Question

【题目】如图，中，，以为底边作等腰三角形，，过点作，垂足为，与相交于点，连接．

（1）求证：．

（2）若，，点是射线上的一点，则当点为何处时，的周长最小，并求出此时的周长．

Answer 1

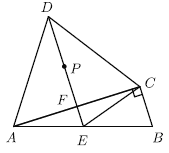
【答案】（1）证明见解析.（2）.

【解析】

（1）首先证明EA=EC，再证明EC=EB即可解决问题．
（2）先说明P与E重合时△PBC的周长最小，最小值=AB+AC．

（1）证明：∵DA=DC，DF⊥AC，
∴AF=CF，
∴DE垂直平分线段AC，
∴EA=EC，
∴∠EAC=∠ECA，
∵∠ACB=90°，
∴∠EAC+∠B=90°，∠ECA+∠ECB=90°，
∴∠ECB=∠B，
∴EC=EB=EA．
（2）连接PB、PC、PA．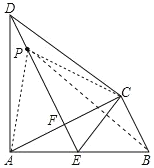

要使得△PBC的周长最小，只要PB+PC最小即可．
∵PB+PC=PA+PB≥AB，
∴当P与E重合时，PA+PB最小，
∴△PBC的周长最小值=AB+BC=15+9=24cm．