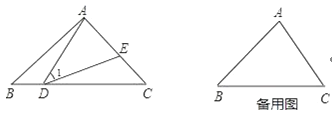
题目内容
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为64和42,则△EDF的面积为 .
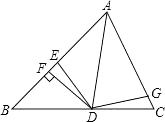
【答案】9
【解析】
试题分析:过点D作DH⊥AC于H,根据角平分线上的点到角的两边距离相等可得DF=DH,再利用“HL”证明Rt△ADF和Rt△ADH全等,Rt△DEF和Rt△DGH全等,然后根据全等三角形的面积相等列方程求解即可.
如图,过点D作DH⊥AC于H, ∵AD是△ABC的角平分线,DF⊥AB, ∴DF=DH,
在Rt△ADF和Rt△ADH中,![]() , ∴Rt△ADF≌Rt△ADH(HL), ∴SRt△ADF=SRt△ADH,
, ∴Rt△ADF≌Rt△ADH(HL), ∴SRt△ADF=SRt△ADH,
在Rt△DEF和Rt△DGH中![]() ,, ∴Rt△DEF≌Rt△DGH(HL), ∴SRt△DEF=SRt△DGH,
,, ∴Rt△DEF≌Rt△DGH(HL), ∴SRt△DEF=SRt△DGH,
∵△ADG和△AED的面积分别为64和42, ∴42+SRt△DEF=64﹣SRt△DGH, ∴SRt△DEF=9.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目