题目内容
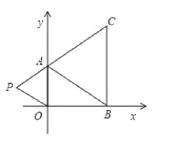
【题目】如图将小球从斜坡的O点抛出,小球的抛出路线可以用二次函数y=ax2+bx刻画,顶点坐标为(4,8),斜坡可以用 ![]() 刻画.
刻画.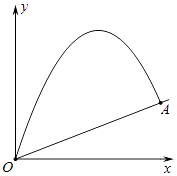
(1)求二次函数解析式;
(2)若小球的落点是A,求点A的坐标;
(3)求小球飞行过程中离坡面的最大高度.
【答案】
(1)解:∵抛物线顶点坐标为(4,8),
∴ 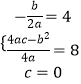 ,
,
解得: 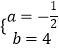 ,
,
∴二次函数解析式为:y=﹣ ![]() x2+4x
x2+4x
(2)解:联立两解析式可得:
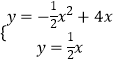 ,
,
解得: ![]() 或
或 ![]() ,
,
∴点A的坐标是(7, ![]() )
)
(3)解:设小球离斜坡的铅垂高度为z,则z=﹣ ![]() x2+4x﹣
x2+4x﹣ ![]() x=﹣
x=﹣ ![]() (x﹣3.5)2+
(x﹣3.5)2+ ![]() ,
,
故当小球离点O的水平距离为3.5时,小球离斜坡的铅垂高度最大,最大值是 ![]()
【解析】(1)依据抛物线的顶点坐标公式可建立过于a,b的二元一次方程组,故此可求出a,b的值,于是可得到抛物线的解析式;
(2)联立直线与抛物线的解析式,通过解方程组可求出交点A的坐标;
(3)设小球飞行过程中离坡面距离为z,则Z=y抛物线-y直线,最后,利用配方法求解即可.

练习册系列答案
相关题目