Question

【题目】如图，在平面直角坐标系中，O为坐标原点，点A（4，1），B（1，1）C（4，5），D（6，﹣3），E（﹣2，5）

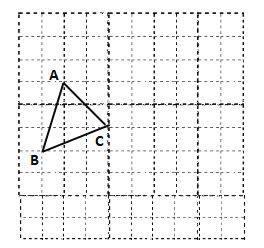
（1）在坐标系中描出各点，画出△AEC，△BCD．

（2）求出△AEC的面积（简要写明简答过程）．

Answer 1

【答案】（1）见解析；（2）△AEC的面积是：12，过程见解析

【解析】

（1）根据各点坐标描出点的位置，依次连接即可；

（2）根据三角形面积公式计算可得．

解：（1）根据各点坐标描出点的位置，依次连接，如图所示：△AEC和△BCD即为所求

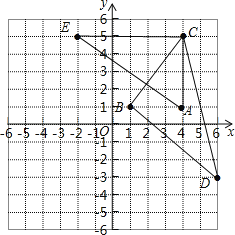
（2）∵A、C的横坐标相同，E、C的纵坐标相同

∴AC⊥x轴，CE平行x轴

∴AC⊥CE

∴△AEC为直角三角形

∴△AEC取EC为底，则EC为6，EC边上高AC＝4

所以S△AEC＝×6×4＝12．