题目内容
【题目】如图所示,在平面真角坐标系中,点A.B的坐标分别为A(a,0),B(b,0),且a,b满足|a+1|+![]() =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3).
(1)求a,b的值及S△ABC;
(2)若点M在x轴上,且S△ACM=![]() S△ABC,试求点M的坐标.
S△ABC,试求点M的坐标.
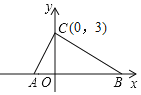
【答案】(1)a=﹣1,b=5,S△ABC=9;(2)M的坐标为(1,0)或(﹣3,0)
【解析】
(1)由|a+1|+![]() =0结合绝对值、算术平方根的非负性即可得出a、b的值,再结合三角形的面积公式即可求出S△ABC的值;
=0结合绝对值、算术平方根的非负性即可得出a、b的值,再结合三角形的面积公式即可求出S△ABC的值;
(2)设出点M的坐标,找出线段AM的长度,根据三角形的面积公式结合S△ACM=![]() S△ABC,即可得出点M的坐标.
S△ABC,即可得出点M的坐标.
解:(1)由|a+1|+![]() =0,|a+1|≥0,
=0,|a+1|≥0,![]() ≥0
≥0
∴a+1=0,b﹣5=0,
∴a=﹣1,b=5,
∴点A(﹣1,0),点B(5,0).
又∵点C(0,3),
∴AB=|﹣1﹣5|=6,CO=3,
∴S△ABC=![]() ABCO=
ABCO=![]() ×6×3=9.
×6×3=9.
(2)设点M的坐标为(x,0),则AM=|x﹣(﹣1)|=|x+1|,
又∵S△ACM=![]() S△ABC,
S△ABC,
∴![]() AMOC=
AMOC=![]() ×9,
×9,
∴![]() |x+1|×3=3,
|x+1|×3=3,
∴|x+1|=2,
即x+1=±2,
解得:x=1或﹣3,
故点M的坐标为(1,0)或(﹣3,0).

练习册系列答案
相关题目
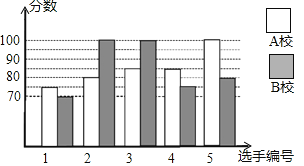
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
![]() 根据图示填写下表:
根据图示填写下表:
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
![]() 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
![]() 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.