题目内容
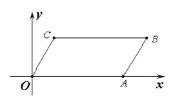
【题目】如图, ![]() OABC的顶点O,A,C的坐标分别是(0,0),(2,0),(
OABC的顶点O,A,C的坐标分别是(0,0),(2,0),(![]() ,1),则点B的坐标是( )
,1),则点B的坐标是( )
A.(1,2)B.(![]() ,2)C.(
,2)C.(![]() ,1)D.(3,1)
,1)D.(3,1)
【答案】C
【解析】
根据平行四边形的性质可证△CDO≌△BEA,得出CD=BE,OD=AE,再由已知条件计算得出BE,OE的长度即可.
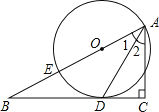
解:过点C作CD⊥OA于点D,过点B作BE⊥OA于点E,
∴∠CDO=∠BEA=90°,
∵四边形OABC是平行四边形,
∴OC=AB,OC∥AB,
∴∠COD=∠BAE
∴在△CDO与△BEA中,
CO=AB,∠COD=∠BAE,∠CDO=∠BEA=90°,
∴△CDO≌△BEA(AAS),
∴CD=BE,OD=AE,
又∵O,A,C的坐标分别是(0,0),(2,0),(![]() ,1)
,1)
∴OD=![]() ,CD=1,OA=2,
,CD=1,OA=2,
∴BE=CD=1,AE=OD=![]() ,
,
∴OE=2+![]() =
=![]() ,
,
∴点B坐标为:(![]() ,1),
,1),
故答案为:C


练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目