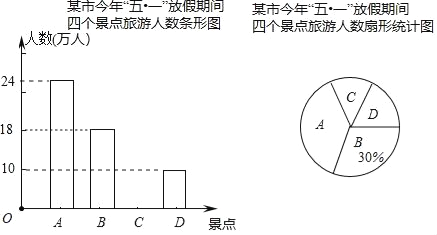
Ő‚ńŅńŕ»›
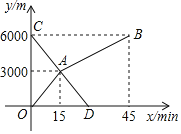
°ĺŐ‚ńŅ°Ņ–°ŃŠļÕĶ‹Ķ‹–°∂ę∑÷Īūī”ľ“ļÕÕľ ťĻ›Õ¨ Ī≥Ų∑Ę£¨—ōÕ¨“ĽŐű¬∑ŌŗŌÚ∂Ý––£¨–°ŃŠŅ™ ľŇ‹≤Ĺ£¨»Ľļůłńő™≤Ĺ––£¨ĶĹīÔÕľ ťĻ›«°ļ√”√45min£ļ–°∂ę∆Ô◊‘––≥Ķ“‘300m/minĶńňŔ∂»÷ĪĹ”Ľōľ“£¨ŃĹ»ňņŽľ“Ķń¬∑≥Őy£®m£©”Žłų◊‘ņŽŅ™≥Ų∑ĘĶōĶń Īľšx£®min£©÷ģľšĶńļĮ żÕľŌů»ÁÕľňý ĺ£ģ
£®1£©ľ“”ŽÕľ ťĻ›÷ģľšĶń¬∑≥Őő™°° °°m£¨–°∂ęī”Õľ ťĻ›ĶĹľ“ňý”√Ķń Īľšő™°° °°£ģ
£®2£©«ů–°ŃŠ≤Ĺ–– Īy”Žx÷ģľšĶńļĮ żĻōŌĶ Ĺ£ģ
£®3£©«ůŃĹ»ňŌŗ”ŲĶń Īľš£ģ
°ĺīūįł°Ņ£®1£©6000,20min£Ľ£®2£©y£Ĺ100x+1500£Ľ£®3£©ŃĹ»ňŌŗ”ŲĶń Īľš «Ķŕ12min
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›ļĮ żÕľŌů÷–Ķń żĺ›Ņ…“‘÷ĪĹ”–ī≥Ųľ“”ŽÕľ ťĻ›÷ģľšĶń¬∑≥Ő£¨ņŻ”√ Īľš=¬∑≥Ő°¬ňŔ∂»ľ∆ň„≥Ų–°∂ęī”Õľ ťĻ›ĶĹľ“ňý”√Ķń Īľš£Ľ
£®2£©łýĺ›ļĮ żÕľŌů÷–Ķń żĺ›ņŻ”√īż∂®ŌĶ ż∑®Ņ…“‘«ůĶ√–°ŃŠ≤Ĺ–– Īy”Žx÷ģľšĶńļĮ żĻōŌĶ Ĺ£Ľ
£®3£©łýĺ›ļĮ żÕľŌů÷–Ķń żĺ›∑÷ņŗŐ÷¬Ř≤ĘŃ–≥Ų∂‘”¶Ķń∑Ĺ≥ŐŅ…“‘ľ∆ň„≥ŲŃĹ»ňŌŗ”ŲĶń Īľš£ģ
Ĺ‚£ļ£®1£©”…ÕľŅ…Ķ√£¨
ľ“”ŽÕľ ťĻ›÷ģľšĶń¬∑≥Őő™6000m£¨–°∂ęī”Õľ ťĻ›ĶĹľ“ňý”√Ķń Īľšő™£ļ![]() £®min£©£¨
£®min£©£¨
Ļ īūįłő™£ļ6000£¨20min£Ľ
£®2£©…Ť–°ŃŠ≤Ĺ–– Īy”Žx÷ģľšĶńļĮ żĻōŌĶ Ĺ «y£Ĺkx+b£¨
Ĺę£®15,3000£©ļÕ£®45,6000£©īķ»Ž£¨Ķ√
![]() £¨
£¨
Ĺ‚Ķ√![]() £¨
£¨
ľī–°ŃŠ≤Ĺ–– Īy”Žx÷ģľšĶńļĮ żĻōŌĶ Ĺ «y£Ĺ100x+1500£Ľ
£®3£©ĶĪ0°‹x°‹15 Ī£¨ľī–°ŃŠŇ‹≤Ĺ Ī”ŽĶ‹Ķ‹Ōŗ”Ų
–°ŃŠĶńňŔ∂»ő™3000°¬15£Ĺ200£®m/min£©£¨
ŃÓ200x+300x£Ĺ6000£¨Ķ√x£Ĺ12£¨
°Ŗ12£ľ15£¨
°ŗŃĹ»ň‘ŕĶŕ12minŌŗ”Ų£¨
ĶĪ15°‹x°‹20 Ī£¨ľī–°ŃŠ≤Ĺ–– Ī”ŽĶ‹Ķ‹Ōŗ”Ų
īň Ī100x+1500=300x
Ĺ‚Ķ√£ļx=![]() £®≤Ľ∑ŻļŌ«įŐŠŐűľĢ£¨Ļ …Š»•£©
£®≤Ľ∑ŻļŌ«įŐŠŐűľĢ£¨Ļ …Š»•£©
īū£ļŃĹ»ňŌŗ”ŲĶń Īľš «Ķŕ12min£ģ