题目内容
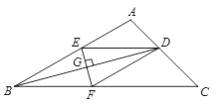
【题目】如图,在△ABC中,BD平分∠ABC交AC于D,EF垂直平分BD,分别交AB,BC,BD于E,F,G,连接DE,DF.
(1)求证:DE=DF;
(2)若∠ABC=30°,∠C=45°,DE=4,求CF的长.
【答案】(1)证明见解析;
(2)CF的长为2+![]()
【解析】试题分析:(1)本题利用垂直平分线的性质,角平分线的性质得出结论,证明四边形BFDE为菱形即可;(2)本题要根据菱形得出三角形DFC的角的度数,作垂直构造特殊的三角形解决问题即可.
试题解析:(1)证明:∵EF垂直平分BD,
∴EB=ED,FB=FD.
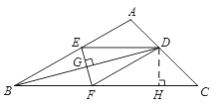
∵BD平分∠ABC交AC于D,
∴∠ABD=∠CBD.
∵∠ABD+∠BEG=90°,∠CBD+∠BFG=90°,
∴∠BEG=∠BFG.
∴BE=BF.
∴四边形BFDE是菱形.
∴DE=DF.
(2)解:过D作DH⊥CF于H.
∵四边形BFDE是菱形,
∴DF∥AB,DE=DF=4.
在Rt△DFH中,∠DFC=∠ABC=30°,
∴DH=2.
∴FH=![]() .
.
在Rt△CDH中,∠C=45°,
∴DH=HC=2.
∴CF=2+![]() .
.

练习册系列答案
相关题目