题目内容
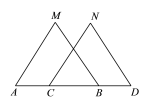
【题目】如图,已知点A、C、B、D在同一条直线上,AC=BD,AM=CN,BM=DN,
求证:(1)△ABM ≌△CDN; (2)AM∥CN.
【答案】(1)见解析;(2)见解析
【解析】
(1)首先根据AC=BD可得AB=CD,再加上条件AM=CN,BM=DN可利用SSS定理证明△AMB≌△CND.
(2) 首先根据AC=BD可得AB=CD,再加上条件AM=CN,BM=DN可利用SSS定理证明△AMB≌△CND,再根据全等三角形的性质可得∠A=∠NCD,即可证明AM∥CN.
解:(1)证明:∵AC=BD,
∴AC+CB=DB+CB,
即:AB=CD,
AC=BD在△AMB和△CND中,
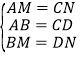 ,
,
∴△AMB≌△CND(SSS).
(2) 证明:∵AC=BD,
∴AC+CB=DB+CB,
即:AB=CD,
AC=BD在△AMB和△CND中,
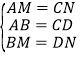 ,
,
∴△AMB≌△CND(SSS),
∴∠A=∠NCD,
∴AM∥CN.

练习册系列答案
相关题目