题目内容
A、B两码头相距150千米,甲客船顺流由A航行到B,乙客船逆流由B到A,若甲、乙两客船在静水中的速度相同,同时出发,它们航行的路程y(千米)与航行时间x(时)的关系如图所示.
(1)求客船在静水中的速度及水流速度;
(2)一艘货轮由A码头顺流航行到B码头,货轮比客船早2小时出发,货轮在静水中的速度为10千米/时,在此坐标系中画出货轮航程y(千米)与时间x(时)的关系图象,并求货轮与客船乙相遇时距A码头的路程。
(1)静水中的速度为20千米/时,水流速度为5千米/时;(2)90千米.
解析试题分析:此题涉及船速,水速,顺风,逆风问题,解答时一定要考虑是顺风还是逆向行驶,不能把净水速误认为是船速,另外会求解函数的解析式,会画简单的函数图形.(1)由图象中路程与时间的关系可得客船在静水中的顺水,逆水速度,由于两客船在静水中的速度相同,又知水流速度不变,进而可得到关于速度的关系,可求解静水中的速度及水速;(2)货轮顺风行驶,可得其速度,由有时间关系可得货轮行驶的函数关系式,进而可求解客轮与货轮之间距离的问题.
试题解析:
解:(1)由图象知,甲船顺流航行6小时的路程为150千米,所以顺流航行的速度为150÷6 =25千米/时;乙船逆流航行10小时的路程为150千米,所以逆流航行的速度为150÷10 =15千米/时
由于两客船在静水中的速度相同,又知水流速度不变,所以设客船在静水中的速度为a千米/时,水流的速度为b千米/时,列方程组得: ,解得:
,解得:
答:客船在静水中的速度为20千米/时,水流速度为5千米/时.
(2)由题意知,货轮顺流航行的速度为10+5=15(千米/时),又知货轮提前出发两小时,所以该图象过(0,30),(8,150)两点,图象如下图线段DE.设DE的解析式为y=k1x+b1
∵ ,解得:
,解得:
∴直线DE的解析式是:
设BC的解析式为y=k2x+b2
∴ ,解得:
,解得: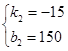
∴BC的解析式为y=-15x+150
解方程组 得
得
答:货轮与客船乙相遇时距A码头的路程是90千米.
考点:一次函数的应用.

某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
| x | 50 | 60 | 90 | 120 |
| y | 40 | 38 | 32 | 26 |
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.

 的解;
的解; 的图象相交于点A(-2,a),并且与x轴相交于点B。
的图象相交于点A(-2,a),并且与x轴相交于点B。
 与
与 的图象相交于A点,函数
的图象相交于A点,函数 轴、
轴、 轴于点B,C,函数
轴于点B,C,函数
 的面积
的面积 与
与 成正比例,且当
成正比例,且当 时,
时, .
. 与
与 的函数关系式;
的函数关系式; 时的函数值.
时的函数值.