题目内容
已知一次函数y=kx+b与y=mx+n的图象如图所示．
（1）写出关于x，y的方程组
的解；
（2）若0<kx+b<mx+n，根据图像写出x的取值范围．
（1）x＝3；y＝4；（2）-1＜x＜1．
解析试题分析：此题主要考查了一次函数与二元一次方程组的关系，一次函数与一元一次不等式组的关系.关键是能利用数形结合掌握方程组的解就是两函数图象的交点．（1）根据方程组的解就是两函数图象的交点求解；（2）用数形结合求出不等式组的取值范围是解答此题的关键．由函数图象可知，当-1＜x＜1时一次函数y1=kx+b的图象在x轴的上方且在一次函数y2=mx+n的图象的下方，故可得出结论．
试题解析：
解：（1）∵一次函数y=kx+b与y=mx+n的图象交于点（3，4），
∴方程组的解为 x＝3 y＝4；
（2）∵当-1＜x＜1时，一次函数y1=kx+b的图象在x轴的上方且在一次函数y2=mx+n的图象的下方，
∴不等式组0＜kx+b＜mx+n的解集是-1＜x＜1．
考点：1、一次函数与二元一次方程（组）；2、一次函数与一元一次不等式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
“节能环保，低碳生活”是我们倡导的一种生活方式，某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台，三种家电的进价和售价如表所示：
| 价格种类 | 进价（元/台） | 售价（元/台） |
| 电视机 | 5000 | 5500 |
| 洗衣机 | 2000 | 2160 |
| 空调 | 2400 | 2700 |
（2）在“2012年消费促进月”促销活动期间，商家针对这三种节能型产品推出“现金每购1000元送50元家电消费券一张、多买多送”的活动.在（1）的条件下，若三种电器在活动期间全部售出，商家预估最多送出多少张？
与函数
的图象大致如图.若
试确定自变量
的取值范围.
＋2与x轴、y轴分别交于A、B两点，以AB为边在第二象限内作正方形ABCD.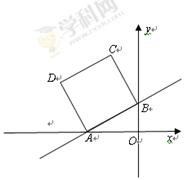
，第一批产品
与上市时间的关系式；
和直线y=kx+b交于A，B两点，点A的坐标为（﹣3，2），BC⊥y轴于点C，且OC=6BC．
的解集．
