题目内容
【题目】今年入夏以来,由于持续暴雨,某县遭受严重洪涝灾害,群众顿失家园。该县民政局为解决群众困难, 紧急组织了一批救灾帐篷和食品准备送到灾区。已知这批物资中,帐篷和食品共 640 件,且帐篷比食 品多 160 件。
(1)帐篷和食品各有多少件?
(2)现计划租用 A、B 两种货车共 16 辆,一次性将这批物资送到群众手中,已知 A 种货车可装帐蓬40 件和食品 10 件,B 种货车可装帐篷 20 件和食品 20 件,试通过计算帮助民政局设计几种运输 方案?
(3)在(2)条件下,A 种货 车每辆需付运费 800 元,B 种货车每辆需付运费 720 元,民政局应选择 哪种方案,才能使运输费用最少?最少费用是多少?
【答案】(1)帐篷有400件,食品有240件;(2)有5种方案:A种车分别为4,5,6,7,8辆,B种车对应为12,11,10,9,8辆;(3)当A种车4辆时费用最少,为11840元.
【解析】
(1)首先设帐篷有x件,食品有y件,根据已知条件可以列出方程组,解方程组即可求解;
(2)设租用A种货车a辆,则租用B种货车(16-a)辆,根据已知条件可以列出不等式组,解不等式组即可求解;
(3)设总费用为W元,则根据已知条件列出函数解析式W=800a+720(16-a)=80a+11520,然后利用一次函数的性质和(2)的结论即可求解.
解:(1)设帐篷有x件,食品有y件,由题意得
![]() ,
,
解得![]() ,
,
答:帐篷有400件,食品有240件;
(2)设租用A种货车a辆,则租用B种货车(16-a)辆,
则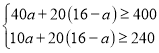 ,
,
解得4≤a≤8,
故有5种方案:A种车分别为4,5,6,7,8辆,B种车对应为12,11,10,9,8辆;
(3)设总费用为W元,则
W=800a+720(16-a)=80a+11520,
k=80>0,W随a的增大而增大,
所以当a=4时费用最少,为11840元.