Question

【题目】如图，矩形ABCD中，AB＝6，AD＝2，E是边CD上一点，将△ADE沿直线AE折叠得到△AFE，BF的延长线交边CD于点G，则DG的最大值为_____．

Answer 1

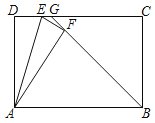
【答案】2

【解析】

如图，以点A为圆心、AD为半径画弧，过点B作弧的切线交CD于点G，切点为F；当点E和点G重合时，DG的最大值即为DE的长；最后根据矩形性质和勾股定理即可解答．

解：如图，以点A为圆心，AD长为半径画弧，

过点B作弧的切线交CD于点G，切点为F，

此时点E和点G重合

DG的最大值即为DE的长．

∵BC＝AD＝2，

AB＝CD＝6，

根据翻折可知：

DE＝EF＝x，

AF＝AD＝2，

则CE＝CD﹣DE＝6﹣x，

在Rt△ABF中，根据勾股定理，得

BF＝＝4，

则BE＝BF+EF＝4+x，

在Rt△BEC中，根据勾股定理，得

（4+x）2＝（6﹣x）2+（2）2，

解得x＝2．

则DG的最大值为2．

故答案为2．