Question

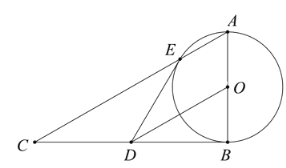
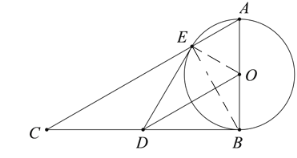
【题目】如图，直角三角形ABC中，∠ABC＝90°，以边AB为直径作圆O，交AC于点E，点D是BC的中点，连接DE

（1）判断DE与圆O的关系，说明理由；

（2）若AB＝4，DE＝，点G是圆上出E、B外的任意一点，则∠EGB＝______°（直接写出答案）．

Answer 1

【答案】（1）相切，证明见解析；（2）120°或60°

【解析】

(1)连接OE,BE，由题意可知OD是三角形ABC的中位线，ED是直角三角形CEB斜边上的中线，从而易得∠EDO=∠BDO，ED=BD，又OD=OD，从而证得EDOBDO，

则∠DEO=∠DBO=90°，即可得到DE与圆O的位置关系；

(2)在直角三角形BDO中，由OB=AB＝2，DB=DE＝，易求出∠ODB=30°，所以∠BOE=120°，在分情况讨论G在弧BE或是弧EAB上两种情况求∠EGB的度数．

(1)DE是圆O的切线.说明如下：

连接OE,BE

∵AB是圆O的直径，

∴∠AEB=90°

∵D是BC的中点，

∴DE=CD=DB

∴∠CED=∠C

又∵AO=OB,

∴OD为三角形ABC的中位线

∴ODAC

∴∠BDO=∠C，∠CED=∠EDO

∴∠BDO=∠EDO

又OD=OD，

∴EDOBDO

∴∠DEO=∠DBO=90°

∴DE是圆O的切线．

(2) 在直角三角形BDO中，由OB=AB＝2，DB=DE＝,

∴tan∠ODB==，

∴∠ODB=30°．

∴∠BOD=60°．

由（1）得EDOBDO，∴∠EOD=∠BOD=60°，即∠BOE=120°．

当G在弧EAB上时，∠EGB =∠BOE=60°．

当G在弧BE上时，∠EGB=180°-60°=120°．

故∠EGB＝60°或120°．