题目内容
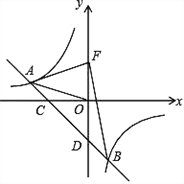
【题目】如图,一次函数 yax 2(a0) 的图象与反比例函数 y![]() (k0) 的图象交于 A、B两点,且与x轴、y轴分别交于点C、D.已知 tan∠AOC=
(k0) 的图象交于 A、B两点,且与x轴、y轴分别交于点C、D.已知 tan∠AOC=![]() ,AO=
,AO=![]() .
.
(1)求这个一次函数和反比例函数的解析式;
(2) 若点 F 是点D 关于 x 轴的对称点,求△ABF 的面积.
【答案】(1)y=﹣![]() ,y=﹣x﹣2;(2)8
,y=﹣x﹣2;(2)8
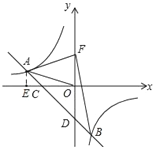
【解析】分析:(1)先过点A作AE⊥x轴于E,构造Rt△AOE,再根据tan∠AOC=![]() ,AO=
,AO=![]() ,求得AE=1,OE=3,即可得出A(-3,1),进而运用待定系数法,求得一次函数和反比例函数的解析式;
,求得AE=1,OE=3,即可得出A(-3,1),进而运用待定系数法,求得一次函数和反比例函数的解析式;
(2)先点F是点D关于x轴的对称点,求得F(0,2),再根据解方程组求得B(1,-3),最后根据△ABF的面积=△ADF面积+△BDF面积,进行计算即可.
详解:(1)过点A作AE⊥x轴于E,
∵tan∠AOC=![]() ,AO=
,AO=![]() ,
,
∴Rt△AOE中,AE=1,OE=3,
∵点A在第二象限,
∴A(﹣3,1),
∵反比例函数y=![]() (k≠0)的图象过点A,
(k≠0)的图象过点A,
∴k=﹣3×1=﹣3,
∴反比例函数的解析式为y=﹣![]() ,
,
∵一次函数y=ax﹣2(a≠0)的图象过点A,
∴1=﹣3a﹣2,
解得a=﹣1,
∴一次函数的解析式为y=﹣x﹣2;
(2)一次函数的解析式y=﹣x﹣2中,令x=0,则y=﹣2,
∴D(0,﹣2),
∵点F是点D关于x轴的对称点,
∴F(0,2),
∴DF=2+2=4,
解方程组 ,可得
,可得![]() 或
或![]() ,
,
∴B(1,﹣3),
∵△ADF面积=![]() ×DF×CE=6,
×DF×CE=6,
△BDF面积=![]() ×DF×|xB|=2,
×DF×|xB|=2,
∴△ABF的面积=△ADF面积+△BDF面积=6+2=8.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目