题目内容
【题目】在△ABC中,AB=4,BC=6,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
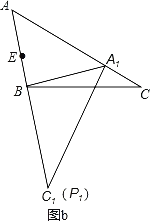
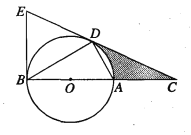
(2)如图2,连接AA1,CC1.若△CBC1的面积为3,求△ABA1的面积;
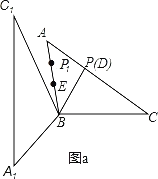
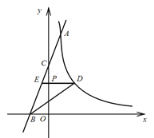
(3)如图3,点E为线段AB中点,点P是线段AC上的动点.在△ABC绕点B按逆时针方向旋转的过程中,点P的对应点是点P1,直接写出线段EP1长度的最大值与最小值.

【答案】(1)∠CC1A1=60°;(2)![]() ;(3)线段EP1长度的最大值为8,EP1长度的最小值1.
;(3)线段EP1长度的最大值为8,EP1长度的最小值1.
【解析】
(1)由由旋转的性质可得:∠A1C1B=∠ACB=30°,BC=BC1,又由等腰三角形的性质,即可求得∠CC1A1的度数;
(2)由△ABC≌△A1BC1,易证得△ABA1∽△CBC1,然后利用相似三角形的面积比等于相似比的平方,即可求得△ABA1的面积;
(3)由①当P在AC上运动至垂足点D,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小;②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,即可求得线段EP1长度的最大值与最小值.
(1)如图1,依题意得:△A1C1B≌△ACB,
∴BC1=BC,∠A1C1B=∠C=30°,
∴∠BC1C=∠C=30°,
∴∠CC1A1=60°;
(2)如图2,由(1)知:△A1C1B≌△ACB,
∴A1B=AB,BC1=BC,∠A1BC1=∠ABC,
∴∠ABA1=∠CBC1,![]() ,
,
∴△A1BA∽△C1BC,∴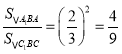
∵![]() ,
,
∴![]() ;
;
(3)线段EP1长度的最大值为8,EP1长度的最小值1.
过程如下:①如图a,过点B作BD⊥AC,D为垂足.
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=6×![]() =3,
=3,
当点P在AC上运动,BP与AC垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1﹣BE=BD﹣BE=3﹣2=1;
②当点P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BC+BE=6+2=8.
综上所述:线段EP1长度的最大值为8,EP1长度的最小值1.