题目内容
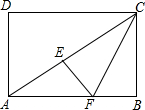
直角三角形纸片的两直角边长分别为6，8，现将△ABC如图那样折叠，使点A与点B重合，折痕为DE，则CE：BE的值为（ ）
A．
| B．
| C．
| D．z=-3x+3000 |
设CE=x，那么AE=8-x，
∵△BDE是△ADE翻折得到的，
∴△BDE≌△ADE，
∴BE=AE=8-x，
在Rt△CBE中，CE2+BC2=BE2，
即x2+62=（8-x）2，
解得x=
，
即CE=
，
∴BE=AE=
，
∴CE：BE=7：25．
故选A．
∵△BDE是△ADE翻折得到的，∴△BDE≌△ADE，
∴BE=AE=8-x，
在Rt△CBE中，CE2+BC2=BE2，
即x2+62=（8-x）2，
解得x=
| 7 |
| 4 |
即CE=
| 7 |
| 4 |
∴BE=AE=
| 25 |
| 4 |
∴CE：BE=7：25．
故选A．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
