题目内容
【题目】数学活动–探究特殊的平行四边形.
问题情境
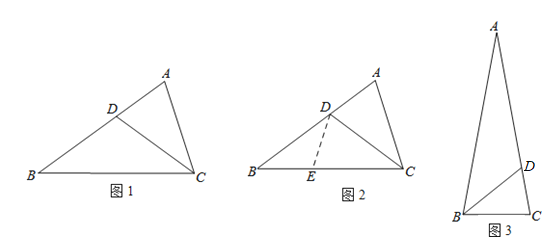
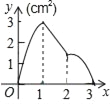
如图,在四边形![]() 中,
中,![]() 为对角线,
为对角线,![]() ,
,![]() .请你添加条件,使它们成为特殊的平行四边形.
.请你添加条件,使它们成为特殊的平行四边形.
提出问题

![]() 第一小组添加的条件是“
第一小组添加的条件是“![]() ”,则四边形
”,则四边形![]() 是菱形.请你证明;
是菱形.请你证明;
![]() 第二小组添加的条件是“
第二小组添加的条件是“![]() ,
,![]() ”,则四边形
”,则四边形![]() 是正方形.请你证明.
是正方形.请你证明.
【答案】见解析
【解析】
(1)先根据SSS定理得出△ABC≌△ADC,故可得出∠BAC=∠DAC,∠BCA=∠DCA.再由AB∥CD可得出∠BAC=∠DCA,根据等边对等角可得出四边形的四条边均相等,进而可得出结论;
(2)根据△ABC≌△ADC得出∠D=∠B,再由∠BCD=90°得出四边形ABCD是矩形,根据BC=DC可得出结论.
![]() 证明:在
证明:在![]() 与
与![]() 中,
中,
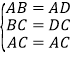 ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形;
是菱形;![]() 解:在
解:在![]() 与
与![]() 中,
中,
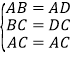 ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∵![]() ,
,
∴四边形![]() 是矩形.
是矩形.
∵![]() ,
,
∴矩形![]() 是正方形.
是正方形.

练习册系列答案
相关题目