题目内容
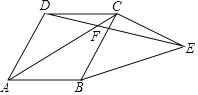
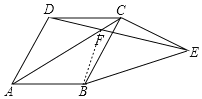
【题目】如图,菱形ABCD的边BC绕点C逆时针旋转90°到CE,连接AC、DE、BE,AC与DE相交于F,则∠AFD=_____.
【答案】45°
【解析】
连接BF,由“SAS”可证△DCF≌△BCF,可得∠CDF=∠CBF,由旋转的性质可得CD=CE,∠CBE=45°,于是∠CDF=∠CED=∠CBF,可证点F,点C,点E,点B四点共圆,即可求解.
解:连接BF,
∵四边形ABCD是菱形,
∴CD=CB,∠DCA=∠BCA,且CF=CF.
∴△DCF≌△BCF(SAS).
∴∠CDF=∠CBF,
∵BC绕点C逆时针旋转90°到CE,
∴BC=CE,∠BCE=90°.
∴CD=CE,∠CBE=45°.
∴∠CDF=∠CED=∠CBF
∴点F,点C,点E,点B四点共圆.
∴∠CFE=∠CBE=45°.
∴∠AFD=45°.
故答案为:45°.

练习册系列答案
相关题目