题目内容
已知：如图，AB为半圆的直径，O为圆心，C为半圆上一点， OE⊥弦AC于点D，交⊙O于点E. 若AC=8cm，DE="2cm." 求OD的长.
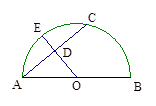
解：∵OE⊥弦AC，
∴AD=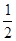
AC=4.
∴OA2=OD2+AD2
∴OA2=(OA-2)2+16
解得，OA="5"
∴OD=3
∴AD=
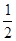AC=4. ∴OA2=OD2+AD2
∴OA2=(OA-2)2+16
解得，OA="5"
∴OD=3
先根据垂径定理求出AD的长，再设OA=r，则OD=OA-DE=r-2，在Rt△AOD中利用勾股定理即可求出OA的长，进而可得出OD的长．
练习册系列答案
名校通行证有效作业系列答案
相关题目
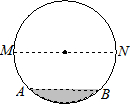
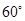的圆心角所对的弦长为 ．
