题目内容
【题目】在平行四边形ABCD中，E是CD上一点，DE：EC=1：3，连AE，BE，BD且AE，BD交于F，则S△DEF：S△EBF：S△ABF= ．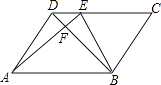 
【答案】1：4：16
【解析】解：∵DE：EC=1：3， ∴DE：DC=1：4，
∵四边形ABCD为平行四边形，
∴DC=AB，DC∥AB，
∴DE：AB=1：4，
∵DE∥AB，
∴△DEF∽△BAF，
∴ 
= 
= 
，
∴ 
= = ， 
=（ ）2= 
，
∴S△DEF：S△EBF：S△ABF=1：4：16．
由DE：EC=1：3得DE：DC=1：4，再根据平行四边形的性质得DC=AB，DC∥AB，则DE：AB=1：4，接着可证明△DEF∽△BAF，根据相似的性质得∴ = = ，根据三角形面积公式可得 = ，根据相似三角形的性质可得 =（ ）2 ， 于是可得S△DEF：S△EBF：S△ABF的值．
练习册系列答案
相关题目
【题目】“五四”期间，小张购进100只两种型号的文具进行销售，其进价和售价之间的关系如下表：
型号 | 进价（元/只） | 售价（元/只） |
A型 | 10 | 12 |
B型 | 15 | 23 |
（1）设购进A型文具x只，销售利润为w元，求w与x的函数关系式？
（2）要使销售文具所获利润最大，且所获利润不超过进货价格的40%，请你帮小张设计一个进货方案，并求出其所获利润的最大值．
