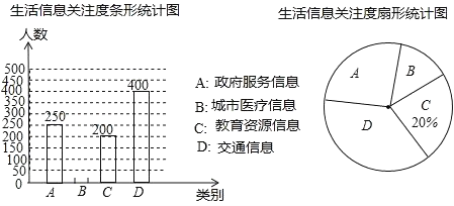
题目内容
【题目】 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=![]() (k>0,x>0)的图象上,点D的坐标为(2,
(k>0,x>0)的图象上,点D的坐标为(2,![]() ),设AB所在直线解析式为y=ax+b(a≠0),
),设AB所在直线解析式为y=ax+b(a≠0),
(1)求k的值,并根据图象直接写出不等式ax+b>![]() 的解集;
的解集;
(2)若将菱形ABCD沿x轴正方向平移m个单位,
①当菱形的顶点B落在反比例函数的图象上时,求m的值;
②在平移中,若反比例函数图象与菱形的边AD始终有交点,求m的取值范围.

【答案】(1)x>2;(2)①![]() ;②
;②![]() .
.
【解析】
(1)根据菱形的性质和D的坐标即可求出A的坐标,代入求出即可;
(2)①点B平移后对应点B′坐标为(m,![]() ),将其代入函数解析式求得m的值;
),将其代入函数解析式求得m的值;
②A和D可能落在反比例函数的图象上,根据平移求出即可.
解:(1)延长AD交x轴于F,由题意得AF⊥x轴
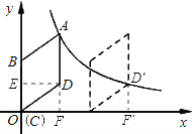
∵点D的坐标为(2,![]() ),
),
∴OF=2,DF=![]() ,
,
∴OD=![]() ,
,
∴AD=![]()
∴点A坐标为(2,4),
∴k=xy=2×4=8,
由图象得解集:x>2;
(2)①将菱形ABCD沿x轴正方向平移m个单位,则平移后B′坐标为(m,![]() ),
),
因B′落在函数![]() (x>0)的图象上,则
(x>0)的图象上,则![]() ;
;
②将菱形ABCD沿x轴正方向平移m个单位,使得点D落在函数![]() (x>0)的图象D′点处,
(x>0)的图象D′点处,
∴点D′的坐标为![]() ,
,
∵点D′在![]() 的图象上,
的图象上,
∴![]() ,
,
解得:![]() ,
,
∴![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目