题目内容
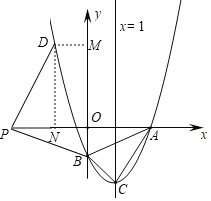
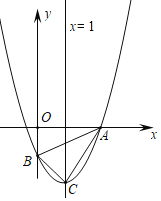
【题目】如图,对称轴为![]() 的抛物线
的抛物线![]() 与x轴交于点
与x轴交于点![]() 与y轴交于点B,顶点为C.
与y轴交于点B,顶点为C.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 若点P在x轴上,将线段BP绕着点P逆时针旋转
若点P在x轴上,将线段BP绕着点P逆时针旋转![]() 得到PD,点D是否会落在抛物线上?如果会,求出点P的坐标;若果不会,说明理由.
得到PD,点D是否会落在抛物线上?如果会,求出点P的坐标;若果不会,说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)![]() ;(3)会,点P坐标为(﹣5,0)或(0,0).
;(3)会,点P坐标为(﹣5,0)或(0,0).
【解析】
(1)抛物线对称轴为x=1,点A(3,0),则抛物线与x轴另外一个交点为(﹣1,0),即可求解;
(2)利用S△ABC![]() CH×OA即可求解;
CH×OA即可求解;
(3)会.如图所示,过点D分别作x、y轴的垂线于点N、M,设点P坐标为(m,0).
证明△DNP≌△POB(AAS),得到PN=OB=3,DN=OP=﹣m,ON=-3-m,得到点D的坐标(m+3,﹣m).将点D坐标代入二次函数表达式,解方程即可得到结论.
(1)抛物线对称轴为x=1,点A(3,0),则抛物线与x轴另外一个交点为(﹣1,0),则抛物线的表达式为:y=(x+1)(x﹣3)=x2﹣2x﹣3;
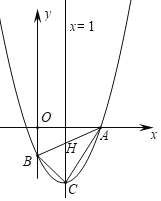
(2)在y=x2﹣2x﹣3中,令x=0,则y=﹣3,即点B(0,﹣3),点C的坐标为(1,﹣4).设对称轴交直线AB与点H,把点B、A坐标代入一次函数表达式:y=kx﹣3得:0=3k﹣3,解得:k=1,则直线BA的表达式为:y=x﹣3,则点H(1,﹣2),S△ABC![]() CH×OA
CH×OA![]() 2×3=3;
2×3=3;
(3)会,理由如下:
如图所示,过点D分别作x、y轴的垂线于点N、M,设点P坐标为(m,0).
∵∠DPN+∠OPB=90°,∠OPB+∠OBP=90°,∴∠OBP=∠DPN,∠DNP=∠BOP=90°,PB=PD,∴△DNP≌△POB(AAS),∴PN=OB=3,DN=OP=﹣m,ON=-3-m,∴N(m+3,0),∴点D的坐标(m+3,﹣m).
将点D坐标代入二次函数表达式得:(m+3)2﹣2(m+3)﹣3=-m,m2+5m=0,解得:m=-5或m=0,∴点P坐标为(﹣5,0)或(0,0).