Question

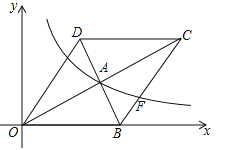
【题目】如图，OA，OB是⊙O的两条半径，OA⊥OB，C是半径OB上的一动点，连接AC并延长交⊙O于D，过点D作直线交OB延长线于E，且DE=CE，已知OA=8．

（1）求证：ED是⊙O的切线；

（2）当∠A=30°时，求CD的长．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

（1）如图连接OD．欲证明DE是切线，只要证明OD⊥DE即可；

（2）解直角三角形求出OC，只要证明CD=OC即可解决问题；

（1）证明：如图连接OD．

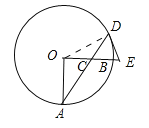
∵OA=OD，∴∠A=∠ODA．

∵OA⊥OB，∴∠AOB=90°，∴∠A+∠ACO=90°．

∵ED=EB，∴∠EDB=∠EBD=∠ACO，∴∠ODA+∠EDC=90°，∴OD⊥DE，∴DE是⊙O的切线．

（2）在Rt△AOC中，∵OA=8，∠A=30°，∴OC=OAtan30°=．

∵OA=OD，∴∠ODA=∠A=30°，∠DOA=120°，∠DOC=30°，∴∠DOC=∠ODC=30°，∴CD=OC=．