Question

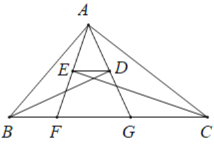
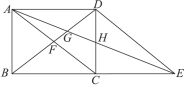
【题目】如图，在矩形ABCD中对角线AC，BD相交于点F，延长BC到点E，使得四边形ACED是一个平行四边形，平行四边形对角线AE交BD，CD分别为点G和点H.

(1)证明：DG2＝FG·BG；

(2)若AB＝5，BC＝6，则线段GH的长度．

Answer 1

【答案】（2）见解析（2）

【解析】

（1）由已知可证得△ADG∽△EBG，△AGF∽△EGD，根据相似三角形的对应边成比例即可得到DG2＝FG·BG；

（2）由已知可得到DH，AH的长，又因为△ADG∽△EBG，从而求得AG的长，则根据GH＝AHAG就得到了线段GH的长度．

解：（1）证明：∵ABCD是矩形，且AD∥BC，

∴△ADG∽△EBG．

∴ ．

又∵△AGF∽△EGD，

∴ ．

∴ ．

∴DG2＝FG·BG．

（2）∵ACED为平行四边形，AE，CD相交于点H，

∴DH＝DC＝AB＝，AE=13.

∴在直角三角形ADH中，

∴AH＝

又∵△ADG∽△EBG，

∴ ．

∴AG＝GE＝×AE＝×13＝．

∴GH＝AHAG＝．