题目内容
【题目】设一次函数y=ax+b（a，b是常数，且a≠0）的图象A（1，3）和B（-1，-1）两点．
（1）求该一次函数的表达式．
（2）①若点（
，2）在（1）中的函数图象上，求m的值．
②若（1）中的函数图象和y=-2x+n的函数图象的交点在第一象限，求n的取值范围．
【答案】（1）y=2x+1；（2）①m=3；②n>1．
【解析】
(1)已知一次函数图像经过两点，用待定系数法即可求解函数解析式；
(2) ①把点（
，2）代入一次函数的解析式，即可求出m的值；
②联立两个一次函数的解析式，求出交点坐标，再根据交点在第一象限得到不等式组，求解即可得到答案；
解：(1)∵一次函数y=ax+b的图象A（1，3）和B（-1，-1）两点，
∴
，
解得：
，
∴一次函数的解析式为：y=2x+1；
(2) ①点（ ，2）在y=2x+1的函数图象上，
∴
，
即：
，
∴解得：m=3；
②∵联立y=2x+1和y=-2x+n得到，
，
即：
解得：
，
把代入y=2x+1得到：
，
即：
，
∴交点坐标为：
，
又∵交点在第一象限，
∴
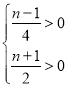，即
解得：
；
练习册系列答案
相关题目
