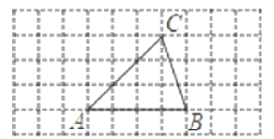Question

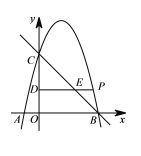
【题目】如图，在平面直角坐标系xOy中，点A的坐标为A（1，0），等腰直角三角形ABC的边AB在x轴的正半轴上，∠ABC＝90°，点B在点A的右侧，点C在第一象限．将△ABC绕点A逆时针旋转75°，如果点C的对应点E恰好落在y轴的正半轴上，那么点C的坐标为_____．

Answer 1

【答案】

【解析】

依据旋转的性质，即可得到∠OAE＝60°，再根据OA＝1，∠EOA＝90°，∠OAE＝60°，即可得出AE＝2，AC＝2．最后在Rt△ABC中，可得到AB和BC，进而求得C点坐标．

解：依题可知，∠BAC＝45°，∠CAE＝75°，AC＝AE，

∴∠OAE＝60°，

在Rt△AOE中，OA＝1，∠EOA＝90°，∠OAE＝60°，

∴AE＝2，

∴AC＝2．

∴在Rt△ABC中，

∴OB＝+1，

∴．

故答案为：．