Question

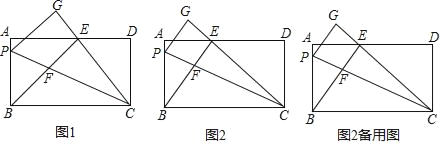
【题目】问题发现：（1）如图1，在等腰直角三角形中，，点为的中点，点为上一点，将射线顺时针旋转交于点，则与的数量关系为____；

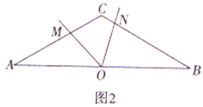
问题探究：（2）如图2，在等腰三角形中，，点为的中点，点为上一点，将射线顺时针旋转交于点，则与的数量关系是否改变，请说明理由；

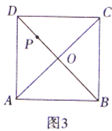
问题解决：（3）如图3，点为正方形对角线的交点，点为的中点，点为直线上一点，将射线顺时针旋转交直线于点，若，当面积为时，直接写出线段的长．

Answer 1

【答案】（1）OM=ON；（2）不改变；证明见解析；（3）线段BN的长为或

【解析】

（1）连接，OC，证明△AOM≌△CON（ASA）可得结论．

（2）数量关系不变．如图2中，过点O作OK⊥AC于K，OJ⊥BC于J，连接OC．证明△OKM≌△OJN（AAS）可得结论．

（3）如图3中，过点P作PG⊥AB于G，PH⊥BC于H．证明△MOC≌△NOB（SAS），推出CM=BN，设CM=BN=m，根据S△PMN==S△PBM+S△BMN-S△PBN，构建方程求解即可．当点M在CB的延长线上时，同法可求．

解：（1）如图1中，结论：OM=ON．

理由：连接OC．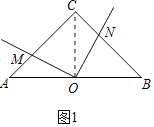

∵CA=CB，∠ACB=90°，AO=OB，
∴CO=OA=OB，OC⊥AB，∠A=∠B=45°，∠BCO=∠ACO=45°
∴∠AOC=∠MON=90°，
∴∠AOM=∠CON，
∵∠A=∠CON，
∴△AOM≌△CON（ASA），
∴OM=ON．
故答案为：OM=ON．

（2）理由：如图2中，过点O作OK⊥AC于K，OJ⊥BC于J，连接OC．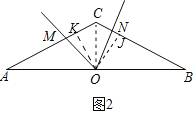

∵∠ACB=120°，∠OKC=∠OJC=90°，
∴∠KOJ=60°=∠MON，
∴∠MKO=∠NOJ，
∵CA=CB，OA=OB，
∴OC平分∠ACB，
∵OK⊥CA，OJ⊥CB，
∴OK=OJ，
∵∠OKM=∠OJN=90°，
∴△OKM≌△OJN（AAS），
∴OM=ON．

（3）如图3中，过点P作PG⊥AB于G，PH⊥BC于H．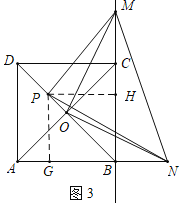

∵四边形ABCD是正方形，
∴AB=AD=4，∠BAD=90°，
∴BD=AB=4，
∴OD=OB=2，PD=OP=，
∴PB=3，
∵四边形PGBH是正方形，
∴PG=PH=3，
∵∠MON=∠COB=90°，
∴∠MOC=∠NOB，
∵OM=ON，OC=OB，
∴△MOC≌△NOB（SAS），
∴CM=BN，设CM=BN=m，
∵S△PMN==S△PBM+S△BMN-S△PBN，
∴（4+m）3+m（4+m）m3=，
∴整理得：m2+4m-13=0，
解得m=或（舍去），
∴BN=．
当点M在CB的延长线上时，同法可得BN=．
综上所述，满足条件的BN的值为或．