题目内容
【题目】定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
(问题理解)
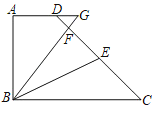
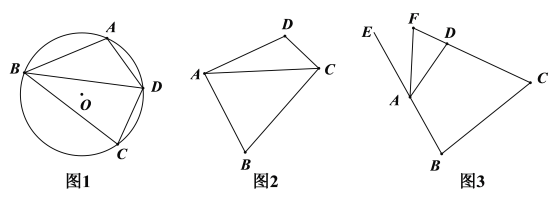
(1)如图1,点A、B、C在⊙O上,∠ABC的平分线交⊙O于点D,连接AD、CD.
求证:四边形ABCD是等补四边形;
(拓展探究)
(2)如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由;
(升华运用)
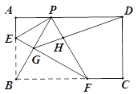
(3)如图3,在等补四边形ABCD中,AB=AD,其外角∠EAD的平分线交CD的延长线于点F.若CD=6,DF=2,求AF的长.
【答案】(1)见解析;(2) AC平分∠BCD,理由见解析;(3) AF=4.
【解析】
(1)由圆内接四边形互补可知∠A+∠C=180°,∠ABC+∠ADC=180°,再证AD=CD,即可根据等补四边形的定义得出结论;
(2)过点A分别作AE⊥BC于点E,AF垂直CD的延长线于点F,证△ABE≌△ADF,得到AE=AF,根据角平分线的判定可得出结论;
(3)连接AC,先证∠EAD=∠BCD,推出∠FCA=∠FAD,再证△ACF∽△DAF,利用相似三角形对应边的比相等可求出AF的长.
(1)证明:∵四边形ABCD为圆内接四边形
∴∠A+∠C=180°,∠ABC+∠ADC=180°.
∵BD平分∠ABC
∴∠ABD=∠CBD
∴弧AD=弧CD
∴AD=CD
∴四边形ABCD是等补四边形
(2)AC平分∠BCD,理由如下:
过点A作AE⊥BC于E,AF⊥CD于F则
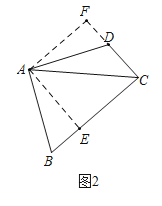
∠AEB=∠AFD=90°
∵四边形ABCD是等补四边形
∴∠ADC+∠B=180°
又∵∠ADC+∠ADF=180°
∴∠B=∠ADF
在△AFD与△AEB中
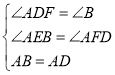
∴![]() ≌
≌![]()
∴![]()
∴点A一定在∠BCD的平分线上
即AC平分∠BCD.
(3)连接AC
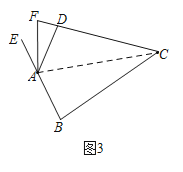
同(2)理得∠EAD=∠BCD
由(2)知AC平分∠BCD所以∠FCA=![]() ∠BCD
∠BCD
同理∠FAD=![]() ∠EAD
∠EAD
∴∠FCA=∠FAD.
又∵∠F=∠F
∴△FAD∽△FCA
∴![]()
即![]()
∴AF=4

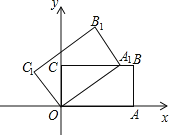
【题目】如图,菱形![]() 的顶点
的顶点![]() 、
、![]() 在
在![]() 轴上(
轴上(![]() 在
在![]() 的左侧),顶点
的左侧),顶点![]() 、
、![]() 在
在![]() 轴上方,对角线
轴上方,对角线![]() 的长是
的长是![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在菱形
在菱形![]() 的边上运动.当点
的边上运动.当点![]() 到
到![]() 所在直线的距离取得最大值时,点
所在直线的距离取得最大值时,点![]() 恰好落在
恰好落在![]() 的中点处,则菱形
的中点处,则菱形![]() 的边长等于( )
的边长等于( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】某校为了解全校学生假期主题阅读的情况(要求每名学生的文章阅读篇数,最少3篇,最多7篇),随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7 |
人数(人) | 20 | 28 |
| 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果,估计该校学生读书总数.