题目内容
【题目】我们知道求函数图象的交点坐标,可以联立两个函数解析式组成方程组,方程组的解就是交点的坐标.如:求直线y=2x+3与y=﹣x+6的交点坐标,我们可以联立两个解析式得到方程组![]() ,解得
,解得![]() ,所以直线y=2x+3与y=﹣x+6的交点坐标为(1,5).请利用上述知识解决下列问题:
,所以直线y=2x+3与y=﹣x+6的交点坐标为(1,5).请利用上述知识解决下列问题:
(1)已知直线y=kx﹣2和抛物线y=x2﹣2x+3,
①当k=4时,求直线与抛物线的交点坐标;
②当k为何值时,直线与抛物线只有一个交点?
(2)已知点A(a,0)是x轴上的动点,B(0,4![]() ),以AB为边在AB右侧做正方形ABCD,当正方形ABCD的边与反比例函数y=
),以AB为边在AB右侧做正方形ABCD,当正方形ABCD的边与反比例函数y=![]() 的图象有4个交点时,试求a的取值范围.
的图象有4个交点时,试求a的取值范围.
【答案】(1)①(1,2),(5,18);②k=﹣2![]() ;(2)a的取值范围是a>2或﹣16<a<﹣4
;(2)a的取值范围是a>2或﹣16<a<﹣4
【解析】
(1)①由题意得: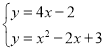 ,解得
,解得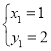 ,
, ,即可求解;
,即可求解;
②利用△=0,即可求解;
(2)分a>0、a<0两种情况,探讨正方形的边与反比例函数图象交点的情况,进而求解.
解:(1)①由题意得: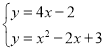 ,解得
,解得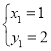 ,
, ,
,
∴直线与抛物线的交点坐标是(1,2),(5,18);
②联立两个函数并整理得:x2﹣(k+2)x+5=0,
△=(﹣k﹣2)2﹣4×5=0,
解得:k=﹣2![]() ;
;
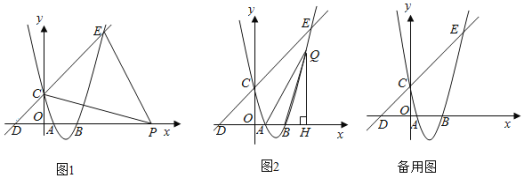
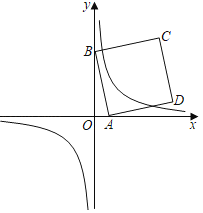
(2)①当a>0时,如图1,
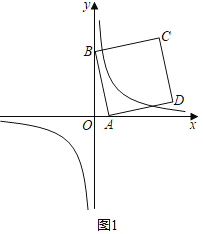
点A、B的坐标分别为:(a,0)、(0,4![]() ),
),
由点A、B的坐标得,直线AB的表达式为:y=﹣![]() x+4
x+4![]() ,
,
当线段AB与双曲线有一个交点时,
联立AB表达式与反比例函数表达式得:﹣![]() x+4
x+4![]() =
=![]() ,
,
整理得:4x2﹣4ax+2a=0,
△=(﹣4a)2﹣16×2a=0,解得:a=2,
故当a>2时,正方形ABCD与反比例函数的图象有4个交点;
②当a<0时,如图2,
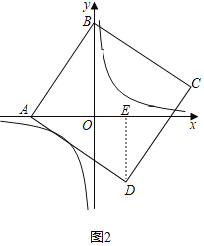
(Ⅰ)当边AD与双曲线有一个交点时,
过点D作ED⊥x轴于点E,
∵∠BAO+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠ADE=∠BAO,
∵AB=AD,∠AOB=∠DEA=90°,
∴△AOB≌△DEA(AAS),
∴ED=AO=﹣a,AE=OB=4![]() ,
,
故点D(a+4![]() ,a),
,a),
由点A、D的坐标可得,直线AD的表达式为:y=![]() a(x﹣a),
a(x﹣a),
联立AD与反比例函数表达式并整理得:ax2﹣a2x﹣16=0,
△=(﹣a2)2﹣4a×(16)=0,解得:a=﹣4(不合题意值已舍去);
(Ⅱ)当边BC与双曲线有一个交点时,
同理可得:a=﹣16,
所以当正方形ABCD的边与反比例函数的图象有4个交点时,a的取值范围为:﹣16<a<﹣4;
综上所述,a的取值范围是a>2或﹣16<a<﹣4.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案