Question

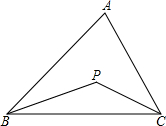
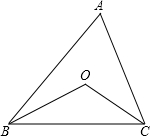
如图，OB、OC分别平分∠ABC和∠ACB，若∠A=60°，则∠O等于（　　）

A．100°

B．120°

C．140°

D．150°

Answer 1

∵OB、OC分别是∠ABC和∠ACB的角平分线，
∴∠OBC+∠OCB=

1

2

∠ABC+

1

2

∠ACB=

1

2

（∠ABC+∠ACB），
∵∠A=60°，
∴∠OBC+∠OCB=

1

2

（180°-60°）=60°，
∴∠BOC=180°-（∠OBC+∠OCB）
=180°-60°
=120°．
故选B．