题目内容
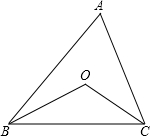
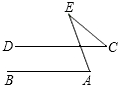
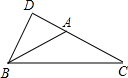
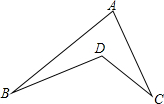
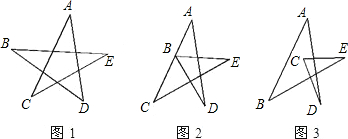
如图1,有一个五角星ABCDE,你能说明∠A+∠B+∠C+∠D+∠E=180°吗?如图2、图3,如果点B向右移到AC上,或AC的另一侧时,上述结论仍然成立吗?请分别说明理由.

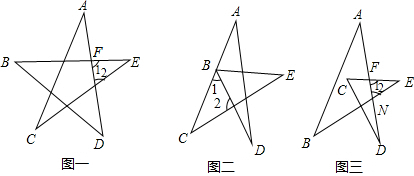
(1)如图(一),∵∠1是△BDF的外角,∴∠B+∠D=∠1,同理∠A+∠C=∠2,由三角形内角和定理可知∠1+∠2+∠E=180°,即,∠B+∠D+∠A+∠C+∠E=180°;
(2)如图(二)∵∠1是△ABD的外角,∴∠A+∠D=∠1,同理∠E+∠EBD=∠2,由三角形内角和定理可知∠1+∠2+∠C=180°,即,∠EBD+∠D+∠A+∠C+∠E=180°;
(3)如图(三),∵∠2是△ABN的外角,∴∠B+∠A=∠2,同理∠D+∠C=∠1,由三角形内角和定理可知∠1+∠2+∠E=180°,即,∠B+∠D+∠A+∠C+∠E=180°,故结论都成立.
(2)如图(二)∵∠1是△ABD的外角,∴∠A+∠D=∠1,同理∠E+∠EBD=∠2,由三角形内角和定理可知∠1+∠2+∠C=180°,即,∠EBD+∠D+∠A+∠C+∠E=180°;
(3)如图(三),∵∠2是△ABN的外角,∴∠B+∠A=∠2,同理∠D+∠C=∠1,由三角形内角和定理可知∠1+∠2+∠E=180°,即,∠B+∠D+∠A+∠C+∠E=180°,故结论都成立.


练习册系列答案
相关题目