题目内容
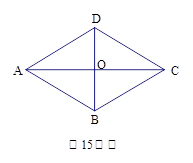
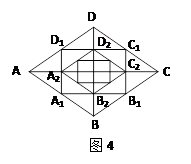
如图4,菱形ABCD的对角线长分别为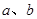 ,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,……,如此下去,得到四边形A2011B2011C2011D2011的面积用含
,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,……,如此下去,得到四边形A2011B2011C2011D2011的面积用含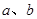 的代数式表示为
的代数式表示为
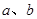 ,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,……,如此下去,得到四边形A2011B2011C2011D2011的面积用含
,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,……,如此下去,得到四边形A2011B2011C2011D2011的面积用含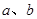 的代数式表示为
的代数式表示为
A.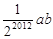 | B. |
C. | D. |
A
专题:规律型.
分析:根据三角形中位线定理,逐步推理出各小长方形的面积,总结出规律,用规律解答.
解答:解:在2009个四边形中,小矩形有2008÷2+1=1005个,根据三角形中位线定理得:
第1个小矩形的面积为
 a×
a× b;
b;第2个小矩形的面积为(
 )2a×(
)2a×( )2b;
)2b;第3个小矩形的面积为(
 )3a×(
)3a×( )3b;
)3b;第4个小矩形的面积为(
 )4a×(
)4a×( )4b;
)4b;…
∴四边形A2011B2011C2011D2011的面积即为:第1006个小矩形的面积(
 )1006a×(
)1006a×( )1006b=
)1006b=(
 )2012ab.,应选A
)2012ab.,应选A点评:此题主要考查学生对菱形的性质及三角形中位线定理的理解及运用.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 的模相等的向量是▼.
的模相等的向量是▼.