题目内容
顺次连接矩形四条边的中点，得到的四边形的形状是▲．
菱形
根据菱形的性质及等腰梯形的性质解答．
解：已知：等腰梯形ABCD中，AD∥BC，AB=CD，E、F、G、H分别是各边的中点，
求证：四边形EFGH是菱形
证明：连接AC、BD
∵E、F分别是AB、BC的中点
∴EF=
AC
同理FG=BD，GH=AC，EH=BD
又∵四边形ABCD是等腰梯形
∴AC=BD
∴EF=FG=GH=HE
∴四边形EFGH是菱形．
解：已知：等腰梯形ABCD中，AD∥BC，AB=CD，E、F、G、H分别是各边的中点，
求证：四边形EFGH是菱形
证明：连接AC、BD
∵E、F分别是AB、BC的中点
∴EF=
AC同理FG=
BD，GH=AC，EH=BD又∵四边形ABCD是等腰梯形
∴AC=BD
∴EF=FG=GH=HE
∴四边形EFGH是菱形．
练习册系列答案
相关题目
的顶点
在原点，点
的坐标为
，点
的纵坐标是
，则顶点
的坐标是 
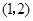
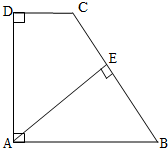
的模相等的向量是▼.