题目内容
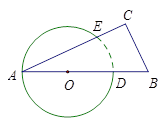
如图矩形ABCD中,过A,B两点的⊙O切CD于E,交BC于F,AH⊥BE于H,连结EF。
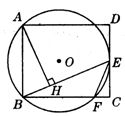
⑴ 求证:∠CEF=∠BAH,⑵若BC=2CE=6,求BF的长。

⑴ 求证:∠CEF=∠BAH,⑵若BC=2CE=6,求BF的长。
(1)弦切角与其弧所对应的的圆周角相等,,再利用等量代换,算出 (2)
(2)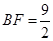
 (2)
(2)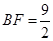
试题分析:(1)证明:∵CE切⊙O于E,∴
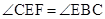 ,
,∵四边形ABCD是矩形,
∴
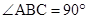
∴
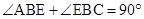 ,
,∵AH丄BE,∴
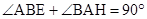
∴
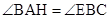 ,∴
,∴
(2)∵CE切⊙O于E ∴CE2=CF·BC,BC=2CE=6
∴
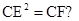 ,所以
,所以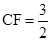 ∴
∴
点评:题目难度不大,学生可以通过多做此类练习,达到举一反三的效果

练习册系列答案
相关题目
 )
)
 B.
B.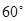 C.
C.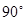 D.
D.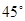
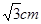 ,则弦CD的长为( )
,则弦CD的长为( )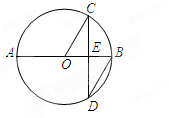
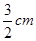

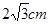
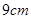
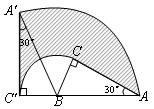
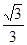 ,坝高为5 m,坝顶CD =" 6" m,现有一工程车需从距B点50 m的A处前方取土,然后经过B—C—D放土,为了安全起见,工程车轮只能停在离A、D处1 m的地方即M、N处工作,已知车轮半经为1 m,求车轮从取土处到放土处圆心从M到N所经过的路径长。(tan150=2-
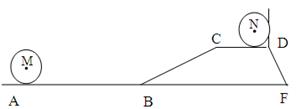
,坝高为5 m,坝顶CD =" 6" m,现有一工程车需从距B点50 m的A处前方取土,然后经过B—C—D放土,为了安全起见,工程车轮只能停在离A、D处1 m的地方即M、N处工作,已知车轮半经为1 m,求车轮从取土处到放土处圆心从M到N所经过的路径长。(tan150=2-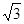 )
)
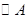 与
与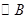 外切,
外切,