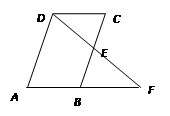题目内容
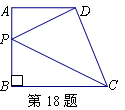
(共8分)如图,在梯形ABCD中,AD∥BC, 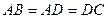 =4,
=4,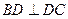 ,E为BC中点,连结DE.
,E为BC中点,连结DE.
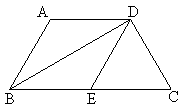
(1)求证:四边形ABED为菱形;(4分)
(2)求梯形ABCD的面积.(4分)
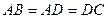 =4,
=4,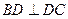 ,E为BC中点,连结DE.
,E为BC中点,连结DE. 
(1)求证:四边形ABED为菱形;(4分)
(2)求梯形ABCD的面积.(4分)
(1)证明略
(2)
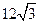
(1)证明:∵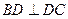 ,E为BC中点
,E为BC中点
∴BE=ED=EC
∴∠DBE=∠BDE
∵AD∥BC,∴∠ADB=∠DBE
∴∠ADB=∠BDE
∵AB=AD,∴∠ABD=∠ADB
∴∠BDE=∠ABD ―――――2分
∴DE∥AB ―――――1分
又∵AD∥BC,即AD∥BE,
∴四边形ABCD为平行四边形 ―――――1分
又AB=AD,∴平行四边形ABCD为菱形.
(2)由(1)得,BE=EC=AD=DE,又∵AD=DC,
∴DE=EC=DC,∴△DEC为等边三角形. ―――――1分
作DF⊥BC于F,则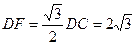 , ―――――1分
, ―――――1分
BC=2BE=2AD=8
∴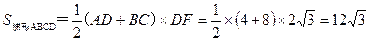 ―――2分
―――2分
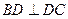 ,E为BC中点
,E为BC中点∴BE=ED=EC
∴∠DBE=∠BDE
∵AD∥BC,∴∠ADB=∠DBE
∴∠ADB=∠BDE
∵AB=AD,∴∠ABD=∠ADB
∴∠BDE=∠ABD ―――――2分
∴DE∥AB ―――――1分
又∵AD∥BC,即AD∥BE,
∴四边形ABCD为平行四边形 ―――――1分
又AB=AD,∴平行四边形ABCD为菱形.
(2)由(1)得,BE=EC=AD=DE,又∵AD=DC,
∴DE=EC=DC,∴△DEC为等边三角形. ―――――1分
作DF⊥BC于F,则
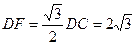 , ―――――1分
, ―――――1分BC=2BE=2AD=8
∴
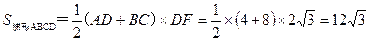 ―――2分
―――2分
练习册系列答案
相关题目
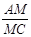 的值是 ▲ .
的值是 ▲ . 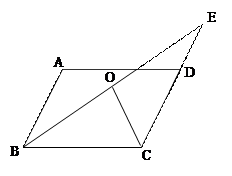
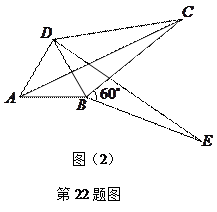
 ,
, ,
,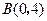 ,请你画出
,请你画出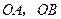 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形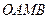 ;
;
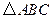 绕顶点
绕顶点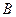 按顺时针方向旋转
按顺时针方向旋转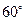 ,得到
,得到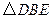 ,连结
,连结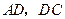 ,
,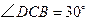 .求证:
.求证: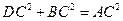 ,即四边形
,即四边形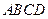 是勾股四边形
是勾股四边形