Question

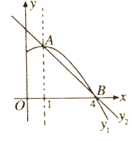
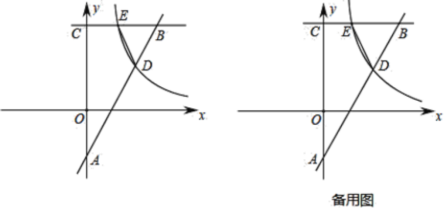
【题目】Rt△OBC在直角坐标系内的位置如图所示，点C在y轴上，∠OCB＝90°，反比例函数y＝(k＞0)在第一象限内的图象与OB边交于点D(m，3)，与BC边交于点E(n，6)．

(1)求m与n的数量关系；

(2)连接CD，若△BCD的面积为12，求反比例函数的解析式和直线OB的解析式；

(3)设点P是线段OB边上的点，在(2)的条件下，是否存在点P，使得以B、C、P为项点的三角形与△BDE相似？若存在，求出此时点P户的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）m＝2n；（2）直线OB的解析式，反比例函数的解析式；（3）点P的坐标为（4，2）；

【解析】

（1）根据点在反比例函数图像上得到方程，即可得到结论；

（2）如图，过点D作DF⊥BC于点F，可得DF=3，根据三角形的面积公式可得BC=8，即可得到结论；

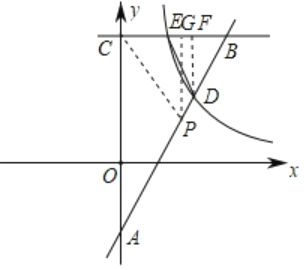
（3）如图，作PG⊥BC于G，①当△BED∽△BCP时，②当△BED∽△BPC时，根据相似三角形的判定和性质即可得到结论．

（1）∵点D(m，3)与E(n，6)在y＝(k＞0)上

∴

∴m与n的数量关系为m＝2n；

（2）如图，过点D作DF⊥BC于点F，可得DF=3，

∴

解得BC=12，

∴B点坐标（12,6）

∴直线OB的解析式；

∵点D(m，3)在OB边上

∴D点坐标(6，3)

∴反比例函数的解析式；

（3）如图，作PG⊥BC于G，由（2）得E点坐标（3,6）

①当△BED∽△BCP时，∠BED＝∠BCP，＝，

∴DF⊥BC，PG⊥BC，

∴DF∥PG，

∴△BDF∽△BPG，

∴＝，

∴＝，即，

∴PG＝4，

∴P（4，2）；

②当△BED∽△BPC时，＝，

∴，

∴BP＝，

∵＝，即．

∴PG＝7.2，此时P不在线段OB上，

综上所述，点P的坐标为（4，2）．