题目内容
【题目】如图,在Rt△ABC中,∠ABC是直角,AB=3,BC=4,P是BC边上的动点,设BP=x,若能在AC边上找到一点Q,使∠BQP=90°,则x的取值范围是 . 
【答案】3≤x≤4
【解析】解:过BP中点O,以BP为直径作圆, 连接QO,当QO⊥AC时,QO最短,即BP最短,
∵∠OQC=∠ABC=90°,∠C=∠C,
∴△ABC∽△OQC,
∴ ![]() ,
,
∵AB=3,BC=4,
∴AC=5,
∵BP=x,
∴QO= ![]() x,CO=4﹣
x,CO=4﹣ ![]() x,
x,
∴ ![]() ,
,
解得:x=3,
当P与C重合时,BP=4,
∴BP=x的取值范围是:3≤x≤4,
所以答案是:3≤x≤4.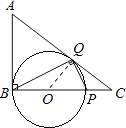
【考点精析】根据题目的已知条件,利用勾股定理的概念和直线与圆的三种位置关系的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边的活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡,改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
x(cm) | 10 | 15 | 20 | 25 | 30 |
y(g) | 30 | 20 | 15 | 12 | 10 |

(1)把上表中(x,y)的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点;
(2)观察所画的图象,猜测y与x之间的函数关系,求出函数关系式并加以验证;
(3)当砝码的质量为24g时,活动托盘B与点O的距离是多少cm?
(4)当活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?