题目内容
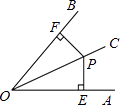
【题目】已知二次函数 ![]() 的图象如图.
的图象如图.
(1)求它的对称轴与x轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
【答案】
(1)
解:由 ![]() ,
,
得x=﹣ ![]() =﹣
=﹣  =3,
=3,
∴D(3,0);
(2)
解:方法一:
如图1,

设平移后的抛物线的解析式为 ![]() ,
,
则C(0,k)OC=k,
令y=0即 ![]() ,
,
得 ![]() ,
, ![]() ,
,
∴A ![]() ,B
,B ![]() ,
,
∴ ![]() ,
,
![]() =2k2+8k+36,
=2k2+8k+36,
∵AC2+BC2=AB2
即:2k2+8k+36=16k+36,
得k1=4,k2=0(舍去),
∴抛物线的解析式为 ![]() ,
,
方法二:
∵ ![]() ,∴顶点坐标
,∴顶点坐标 ![]() ,
,
设抛物线向上平移h个单位,则得到C(0,h),顶点坐标 ![]() ,
,
∴平移后的抛物线: ![]() ,
,
当y=0时, ![]() ,得
,得 ![]() ,
, ![]() ,
,
∴A ![]() ,B
,B ![]() ,
,
∵∠ACB=90°,
∴△AOC∽△COB,则OC2=OAOB,
即 ![]() ,
,
解得h1=4,h2=0(不合题意舍去),
∴平移后的抛物线: ![]() ;
;
(3)
解:方法一:
如图2,

由抛物线的解析式 ![]() 可得,
可得,
A(﹣2,0),B(8,0),C(0,4),M ![]() ,
,
过C、M作直线,连接CD,过M作MH垂直y轴于H,则MH=3,
∴ ![]() ,
,
![]() ,
,
在Rt△COD中,CD= ![]() =AD,
=AD,
∴点C在⊙D上,
∵ ![]()
![]() ,
,
∴DM2=CM2+CD2
∴△CDM是直角三角形,∴CD⊥CM,
∴直线CM与⊙D相切.
方法二:
如图3,

由抛物线的解析式可得A(﹣2,0),B(8,0),C(0,4),M ![]() ,
,
作直线CM,过D作DE⊥CM于E,过M作MH垂直y轴于H,则MH=3, ![]() ,由勾股定理得
,由勾股定理得 ![]() ,
,
∵DM∥OC,
∴∠MCH=∠EMD,
∴Rt△CMH∽Rt△DME,
∴ ![]() 得DE=5,
得DE=5,
由(2)知AB=10,∴⊙D的半径为5.
∴直线CM与⊙D相切.
【解析】(1)根据对称轴公式求出x=﹣ ![]() ,求出即可;(2)假设出平移后的解析式即可得出图象与x轴的交点坐标,再利用勾股定理求出即可;(3)由抛物线的解析式
,求出即可;(2)假设出平移后的解析式即可得出图象与x轴的交点坐标,再利用勾股定理求出即可;(3)由抛物线的解析式 ![]() 可得,A,B,C,M各点的坐标,再利用勾股定理逆定理求出CD⊥CM,即可证明.
可得,A,B,C,M各点的坐标,再利用勾股定理逆定理求出CD⊥CM,即可证明.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边的活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡,改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
x(cm) | 10 | 15 | 20 | 25 | 30 |
y(g) | 30 | 20 | 15 | 12 | 10 |

(1)把上表中(x,y)的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点;
(2)观察所画的图象,猜测y与x之间的函数关系,求出函数关系式并加以验证;
(3)当砝码的质量为24g时,活动托盘B与点O的距离是多少cm?
(4)当活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?