题目内容
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60,OM=4,OQ=1,求证:CN⊥OB.
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问: ![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.

②设菱形OMPQ的面积为S1,△NOC的面积为S2,求![]() 的取值范围.
的取值范围.
【答案】(1)CN⊥OB;(2)①![]() ②0<
②0<![]() ≤
≤![]()
【解析】试题分析:(1)过P作PE⊥OA于E,易证四边形OMPQ为平行四边形.根据三角函数求得PE的长,再根据三角函数求得∠PCE的度数,即可得∠CPM=90,又因PM∥OB,即可证明CN⊥OB.(2)①设OM=x,ON=y,先证△NQP∽△NOC,即可得![]() ,把x,y代入整理即可得
,把x,y代入整理即可得![]() -
-![]() 的值.②过P作PE⊥OA于E,过N作NF⊥OA于F,可得S1=OM·PE,S2=
的值.②过P作PE⊥OA于E,过N作NF⊥OA于F,可得S1=OM·PE,S2=![]() OC·NF,所以
OC·NF,所以![]() =
=![]() .再证△CPM∽△CNO,所以
.再证△CPM∽△CNO,所以![]() =
=![]() =
=![]() ,用x表示出
,用x表示出![]() 与x的关系,根据二次函数的性质即可得
与x的关系,根据二次函数的性质即可得![]() 的取值范围.
的取值范围.
试题解析:(1)
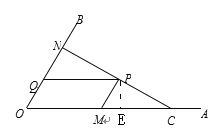
过P作PE⊥OA于E.∵PQ∥OA,PM∥OB,∴四边形OMPQ为平行四边形.
∴PM=OQ=1,∠PME=∠AOB=60,
∴PE=PM·sin60=![]() ,ME=
,ME=![]() ,
,
∴CE=OC-OM-ME=![]() ,∴tan∠PCE=
,∴tan∠PCE=![]() =
=![]() ,
,
∴∠PCE=30,∴∠CPM=90,
又∵PM∥OB,∴∠CNO=∠CPM=90 ,即CN⊥OB.
(2)①![]() -
-![]() 的值不发生变化. 理由如下:
的值不发生变化. 理由如下:
设OM=x,ON=y.∵四边形OMPQ为菱形,∴ OQ=QP=OM=x,NQ=y-x.
∵PQ∥OA,∴∠NQP=∠O.又∵∠QNP=∠ONC,∴△NQP∽△NOC,∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴6y-6x=xy.两边都除以6xy,得![]() -
-![]() =
=![]() ,即
,即![]() -
-![]() =
=![]() .
.
②过P作PE⊥OA于E,过N作NF⊥OA于F,
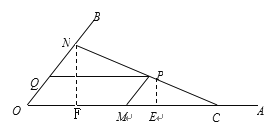
则S1=OM·PE,S2=![]() OC·NF,
OC·NF,
∴![]() =
=![]() .
.
∵PM∥OB,∴∠MCP=∠O.又∵∠PCM=∠NCO,
∴△CPM∽△CNO.∴![]() =
=![]() =
=![]() .
.
∴![]() =
=![]() =-
=-![]() (x-3)2+
(x-3)2+![]() .
.
∵0<x<6,由这个二次函数的图像可知,0<![]() ≤
≤![]() .
.

【题目】甲、乙两位运动员在相同条件下各射靶10次,毎次射靶的成绩情况如图.
(1)请填写下表:
(2)请你从平均数和方差相结合对甲、乙两名运动员6次射靶成绩进行分析:
平均数 | 方差 | 中位数 | 命中9环以上的次数(包括9环) | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 | 7.5 |
(3)教练根据两人的成绩最后选择乙去参加比赛,你能不能说出教练让乙去比赛的理由?(至少说出两条理由)

【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小亮根据学习函数的经验,对函数![]() 的图象与性质进行了探究。
的图象与性质进行了探究。
下面是小亮的探究过程,请补充完整:
(1)函数![]() 中自变量x的取值范围是_________.
中自变量x的取值范围是_________.
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 | 0 |
|
| 2 | 3 | 4 | 5 | … |
y | … | - | - | -4 | -5 | -7 | m | -1 | -2 | - | - | … |
求m的值;
(3)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)根据画出的函数图象,发现下列特征:该函数的图象与直线x=1越来越靠近而永不相交,该函数的图象还与直线_________越来越靠近而永不相交.