��Ŀ����
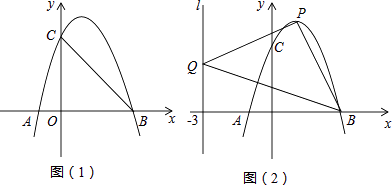
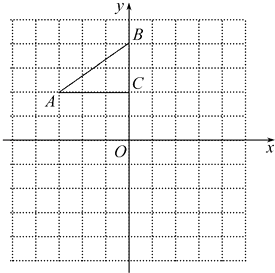
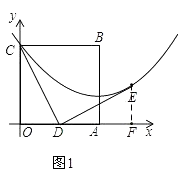
����Ŀ���߳�Ϊ2��������OABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ����D�DZ�OA���е㣬����CD���� E�ڵ�һ���ޣ���DE��DC��DE=DC����ֱ��ABΪ�Գ���������߹�C��E���㣮
��1����E�����ꣻ
��2���������ߵĽ���ʽΪy=a��x��h��2+k����a��h��k��
��3����MΪֱ��AB��һ���㣬��NΪ��������һ���㣬�Ƿ���ڵ�M��N��ʹ���Ե�M��N��D��EΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�����������ĵ�M��N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺����E��EF��x���ڵ�F����ͼ1��
��DE��DC��
���CDO+��EDF=90�㣬
�ߡ�CDO+��OCD=90�㣬
���OCD=��EDF��
�ڡ�COD�͡�DFE��

���COD�ա�DFE��AAS����
��OD=EF��DF=CO��
��CO=OA=2��DΪOA�е㣬
��EF=OD=DA=1��DF=OC=2��
��E��3��1��
��2��
�⣺��������y=a��x��h��2+k��ABΪ�Գ��ᣬ
��h=2��
��y=a��x��h��2+k����C��0��2����E��3��1�����㣬
�� ![]() ��
��
��ã� ![]()
��3��
�⣺������DEΪƽ���ı��εĶԽ��ߣ���ͼ2��

��ʱ��N����������ߵĶ��㣨2�� ![]() ����
����
��N��E������������ֱ��NE�Ľ���ʽΪ��y= ![]() x��
x��
��DM��EN��
����DM�Ľ���ʽΪ��y= ![]() ��
��
��D��1��0����������b=�� ![]() ��
��
��DM�Ľ���ʽΪ��y= ![]() ��
��
��x=2����y= ![]() ��
��
��M��2�� ![]() ����
����
�ڹ���C��CM��DE�������߶Գ����ڵ�M������ME����ͼ3��

��CM��DE��DE��CD��
��CM��CD��
��OC��CB��
���OCD=��BCM��
�ڡ�OCD�͡�BCM��
 ��
��
���OCD�ա�BCM��ASA����
��CM=CD=DE��BM=OD=1��
��CDEM��ƽ���ı��Σ�
��N����Cռ�غϣ�
��N��0��2����M��2��3����
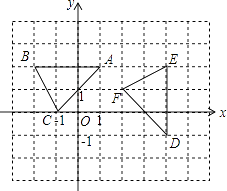
��N���������߶Գ����Ҳ࣬MN��DE����ͼ4��

��NG��BA�ڵ�G���ӳ�DM��BN�ڵ�H��
��MNED��ƽ���ı��Σ�
���MDE=MNE����ENH=��DHB��
��BN��DF��
���ADH=��DHB=��ENH��
���MNB=��EDF��
�ڡ�BMN�͡�FED��

���BMN�ա�FED��AAS����
��BM=EF=1��
BN=DF=2��
��M��2��1����N��4��2����
����������N��M�ֱ��������ʱ���Ե�M��N��D��EΪ������ı�����ƽ���ı���
N��2�� ![]() ����M��2��
����M��2�� ![]() ����
����
N��0��2����M��2��3����
M��2��1����N��4��2��
����������1������E��EF��x���ڵ�F��֤��COD�ա�DFE���ɣ���2��ֱ��AB���ǶԳ��ᣬȷ����h�����C��E�������꣬���������߽���ʽ��ȷ��a��k����3��������������ۣ�N�������߶��㴦��N�������߶Գ�����ࣻN�������߶Գ����Ҳ࣮