题目内容
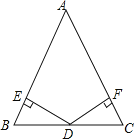
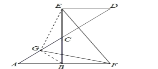
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC,D为斜边AC延长线上一点,过D点作BC的垂线交其延长线于点E,在AB的延长线上取一点F,使得BF=CE,连接EF.
(1)若AB=2,BF=3,求AD的长度;
(2)G为AC中点,连接GF,求证:∠AFG+∠BEF=∠GFE.

【答案】(1)5![]() (2)见详解
(2)见详解
【解析】
(1)易证DE∥AB,可得△ABC∽△DEC,即可证明△CDE为等腰直角三角形,根据CE即可求得CD的长,根据AB可求得AC的长,根据AD=AC+CD即可解题;
(2)连接EG、BG,易证BG=CG,∠ABG=∠ACB=45°,即可证明△GBF≌△GCE,可得GE=GF,∠BGF=∠CGE,∠AFG=∠BEG,即可证明△EFG为等腰直角三角形,可得∠GFE=∠GEF,根据∠GEF=∠BEG+∠BEF即可解题.
(1)∵DE⊥BE,AB⊥BE,
∴DE∥AB,
∴△ABC∽△DEC,
∴△CDE为等腰直角三角形,
∵CE=BF=3,∴CD=3![]() ,
,
∵AB=2,∴AC=2![]() ,
,
∴AD=AC+CD=5![]() ;
;
(2)连接EG、BG,证明△GBF≌△GCE.:∠AFG+∠BEF=∠GFE.
∵G是等腰直角△ABC斜边AC中点,
∴BG=CG,∠ABG=∠ACB=45°,
∴∠GBF=∠GCE=135°,
∵在△GBF和△GCE中, GB=GC,∠GBF=∠GCE,BF=CE,
∴△GBF≌△GCE,(SAS)
∴GE=GF,∠BGF=∠CGE,∠AFG=∠BEG,
∵∠BGF+∠FGC=90°,
∴∠CGE+∠FGC=90°,即∠EGF=90°,
∴△EFG为等腰直角三角形,
∴∠GFE=∠GEF=45°,
∵∠GEF=∠BEG+∠BEF,
∴∠GEF=∠AFG+∠BEF,
∴∠AFG+∠BEF=∠GFE.

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案