题目内容
【题目】已知:如图1,AB=AC,点A是线段DE上一点,∠BAC=90°,BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,你能得到什么结论?并证明你的结论.
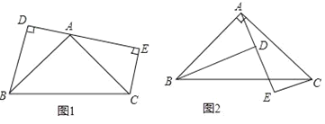
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据全等三角形的判定证明△ADB≌△CEA即可求解;
(2)根据全等三角形的判定证明△ADB≌△CEA,即可得到结论.
证明:(1)∵BD⊥DE,CE⊥DE,
∴∠D=∠E=90°,
∴∠DBA+∠DAB=90°,
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠DBA=∠CAE,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∴DE=AD+AE=CE+BD;
(2)BD=DE+CE,理由是:
∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠ABD+∠EAC=90°,
∴∠BAD=∠EAC,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∵AE=AD+DE,
∴BD=CE+DE.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目