题目内容
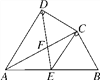
【题目】如图,已知∠AOB,以O为圆心,以任意长为半径作弧,分别交OA,OB于F,E两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证:△FMO≌△FMD.

【答案】(1)32°;(2)见解析.
【解析】
(1)首先根据OB∥FD,可得∠0FD+∠A0B=18O°,进而得到∠AOB的度数,再根据作图可知OP平分∠AOB,进而算出∠DOB的度数即可;
(2)首先证明∴∠A0D=∠ODF,再由FM⊥0D可得∠OMF=∠DMF,再加上公共边FM=FM可利用AAS证明△FMO≌△FMD.
(1)∵OB∥FD,
∴∠0FD+∠A0B=18O°,
又∵∠0FD=116°,
∴∠A0B=180°﹣∠0FD=180°﹣116°=64°,
由作法知,0P是∠A0B的平分线,
∴∠D0B=![]() ∠A0B=32°;
∠A0B=32°;
(2)证明:∵0P平分∠A0B,
∴∠A0D=∠D0B,
∵0B∥FD,
∴∠D0B=∠ODF,
∴∠A0D=∠ODF,
又∵FM⊥0D,
∴∠OMF=∠DMF,
在△MFO和△MFD中
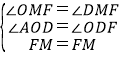 ,
,
∴△MFO≌△MFD(AAS).

【题目】某中学举行“校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出![]() 名选手组成初中代表队和高中代表队参加学校决赛.每个队
名选手组成初中代表队和高中代表队参加学校决赛.每个队![]() 名选手的决赛成绩如图所示:
名选手的决赛成绩如图所示:

![]() 填表:
填表:
平均数(分) | 中位数(分) | 众数(分) | |
初中代表队 |
|
| |
高中代表队 |
|
|
![]() 结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
![]() 计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石.某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:
收费 方式 | 月使用费(元) | 包时上网 时间(h) | 超时费(元/min) |
A | 7 | 25 | 0.6 |
B | 10 | 50 | 0.8 |
设小明每月上网学习人工智能课程的时间为x小时,方案A,B的收费金额分别为yA元,yB元.
(1)当x≥50时,分别求出yA,yB与x之间的函数关系式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?