Question

【题目】已知，点O在线段AB上，AB=6，OC为射线，且∠BOC=45°．动P以每秒1个单位长度的速度从点O出发，沿射线OC做匀速运动．设运动时间为t 秒．

（1）如图1，若AO=2．

①当 t=6秒时，则OP= ，S△ABP= ；

②当△ABP与△PBO相似时，求t的值；

（2）如图2，若点O为线段AB的中点，当AP=AB时，过点A作AQ∥BP，并使得∠QOP=∠B，求AQBP的值．

Answer 1

【答案】（1）①6；；②t=+4；（2）18.

【解析】

试题分析：（1）①如图1中，作PE⊥AB于E．求出PE的长，根据S△APB=ABPE，即可计算．

②如图1中，过点B作OC的垂线，垂足为H，由△ABP∽△PBO，得，即PB2=BOBA=24，推出BP=，再利用勾股定理求出OH、HP即可解决问题．

（2）如图中，作OE∥AP，交BP于点E．由△QAO∽△OEP，得，即AQEP=EOAO，由三角形中位线定理得OE=3，推出AQEP=9，由此即可解决问题．

试题解析：（1）①如图1中，作PE⊥AB于E．

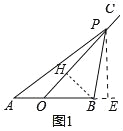
在Rt△OPE中，OP=6，∠POE=45°，

∴PE=OPsin45°=3，

∴S△APB=ABPE=9，

②如图1中，过点B作OC的垂线，垂足为H，

∵△ABP∽△PBO，

∴，

∴PB2=BOBA=24，

∴BP=，

在Rt△OHB中，∵∠BOH=45°，OB=4，

∴OH=HB=，

在Rt△PHB中，PH==4

∴OP=+4，

∴t=+4（秒）时，△ABP∽△PBO．

（2）如图中，作OE∥AP，交BP于点E．

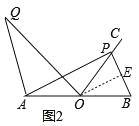
∵AP=AB，

∴∠APB=∠B，

∴∠OEB=∠APB=∠B，

∵AQ∥BP，

∴∠QAB+∠B=180°．

又∵∠OEP+∠OEB=180°，

∴∠OEP=∠QAB，

又∵∠AOC=∠2+∠B=∠1+∠QOP，

∵∠B=∠QOP，

∴∠AOQ=∠OPE，

∴△QAO∽△OEP，

∴，即AQEP=EOAO，

由三角形中位线定理得OE=3，

∴AQEP=9，

AQBP=AQ2EP=2AQEP=18．