题目内容
【题目】如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A、B在x轴上,点C、D在第二象限,点M是BC中点.已知AB=6,AD=8,∠DAB=60°,点B的坐标为(-6,0).
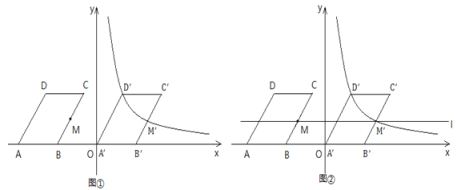
(1)求点D和点M的坐标;
(2)如图①,将□ABCD沿着x轴向右平移a个单位长度,点D的对应点![]() 和点M的对应点
和点M的对应点![]() 恰好在反比例函数
恰好在反比例函数![]() (x>0)的图像上,请求出a的值以及这个反比例函数的表达式;
(x>0)的图像上,请求出a的值以及这个反比例函数的表达式;
(3)如图②,在(2)的条件下,过点M,![]() 作直线l,点P是直线l上的动点,点Q是平面内任意一点,若以
作直线l,点P是直线l上的动点,点Q是平面内任意一点,若以![]() ,P、Q为顶点的四边形是矩形,请直接写出所有满足条件的点Q的坐标.
,P、Q为顶点的四边形是矩形,请直接写出所有满足条件的点Q的坐标.
【答案】(1)D点坐标为![]() ,M点坐标为
,M点坐标为![]() ;(2)a=12,反比例函数解析式为:
;(2)a=12,反比例函数解析式为:![]() ;(3)Q点坐标为
;(3)Q点坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)过点D作DH⊥x轴于点H,求出AH和DH的长,即可求出D点坐标,再根据M为BC中点,求出M的坐标即可;
(2)写出平移后![]() ,
,![]() 的坐标,再根据
的坐标,再根据![]() ,
,![]() 都在反比例函数上,建立方程求出即可;
都在反比例函数上,建立方程求出即可;
(3)设P点坐标为![]() ,分别讨论①当∠
,分别讨论①当∠![]() 90°时,②当∠
90°时,②当∠![]() 90°时,③当∠
90°时,③当∠![]() 90°时,建立方程解出m,从而求出Q点坐标.
90°时,建立方程解出m,从而求出Q点坐标.
(1)过点D作DH⊥x轴于点H,
∵AD=8,∠DAB=60°,
∴AH=4,DH=![]() ,
,
∵AB=6,点B的坐标为(-6,0),
∴H点坐标为(-8,0),
∴D点坐标为![]() ,
,
∵四边形ABCD为平行四边形,
∴C点坐标为![]() ,
,
∵M为BC中点,
∴M点坐标为![]() ;
;

(2)将□ABCD沿着x轴向右平移a个单位长度,
∴![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,
,
∵![]() ,
,![]() 都在反比例函数图像上,
都在反比例函数图像上,
∴把![]() ,
,![]() 代入反比例函数
代入反比例函数![]() 中,得
中,得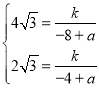 ,
,
解得: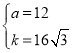 ,
,
∴反比例函数解析式为:![]() ;
;
(3)过点M,![]() 作直线l,
作直线l,
则直线l的解析式为:![]() ,
,
∴设P点坐标为![]() ,
,
由(2)知,
![]() 的坐标为(6,0),
的坐标为(6,0),
![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
若以![]() ,P,Q为顶点的四边形是矩形,分情况讨论:
,P,Q为顶点的四边形是矩形,分情况讨论:
①当∠![]() 90°时,
90°时,
则![]() ,即
,即![]() ,
,
解得:m=16,
则P点坐标为![]() ,
,
则Q点坐标为![]() ;
;
②当∠![]() 90°时,
90°时,
则![]() ,即
,即![]() ,
,
解得:m=0,
则P点坐标为![]() ,
,
则Q点坐标为![]() ;
;
③当∠![]() 90°时,
90°时,
则![]() ,即
,即![]() ,
,
解得: ![]() ,
,
则P点坐标为![]() 或
或![]() ,
,
则对应的Q点坐标为![]() 或
或![]() ;
;
综上,Q点坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.