题目内容
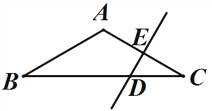
【题目】如图，在△ABC中，AB=AC，∠BAC=120°，DE垂直平分AC，交BC于D，交AC于E，且DE=2cm，求BC的长．
【答案】12cm
【解析】试题分析：首先连接AD，由DE垂直平分AC，根据线段垂直平分线的性质，易得AD=CD，又由在△ABC中，AB=AC，∠BAC=120°，易求得∠DAC=∠B=∠C=30°，继而可得∠BAD=90°，然后利用含30°角的直角三角形的性质，即可求得BC的长．
试题解析：连接AD，
∵DE垂直平分AC，
∴AD=CD，∠DEC=90°，
∴∠DAC=∠C，
∵在△ABC中，AB=AC，∠BAC=120°，
∴∠B=∠C=
=30°，
∴∠DAC=∠C=∠B=30°，
∴∠ADB=∠DAC+∠C=60°，
∴∠BAD=180°-∠B-∠ADB=90°，
在Rt△CDE中，∠C=30°，DE=2cm，
∴CD=2DE=4cm，
∴AD=CD=4cm，
在Rt△BAD中，∠B=30°，
∴BD=2AD=8cm，
∴BC=BD+CD=12（cm）．
练习册系列答案
名校课堂系列答案
相关题目
