Question

【题目】如图，抛物线y=﹣ x2﹣ x+ 与x轴交于A，B两点（A点在B点的左侧），与y轴交于点C，已知点D（0，﹣ ）．

（1）求直线AC的解析式；
（2）如图1，P为直线AC上方抛物线上的一动点，当△PBD面积最大时，过P作PQ⊥x轴于点Q，M为抛物线对称轴上的一动点，过M作y轴的垂线，垂足为点N，连接PM，NQ，求PM+MN+NQ的最小值；
（3）在（2）问的条件下，将得到的△PBQ沿PB翻折得到△PBQ′，将△BPQ′沿直线BD平移，记平移中的△PBQ′为△P′B′Q″，在平移过程中，设直线P′B′与x轴交于点E．则是否存在这样的点E，使得△B′EQ″为等腰三角形？若存在，求此时OE的长．

Answer 1

【答案】
（1）解：∵抛物线y=﹣ x2﹣ x+ 与x轴交于A，B两点（A点在B点的左侧），与y轴交于点C，

∴A（﹣4，0），B（1，0），C（0， ），

设直线AC的解析式为y=kx+b，则有 ，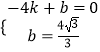

∴k= ，b= ，

∴直线AC的解析式为y= x+

（2）解：如图1中，分别过D、B作x轴，y轴的平行线交于点K，连接PK．设P（m，﹣ m2﹣ m+ ）．

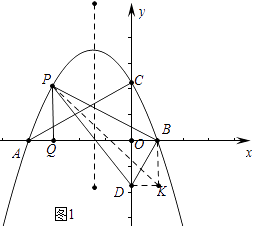
S△PDB=S△PDK+S△PBK﹣S△DKB

= 1（﹣ m2﹣ m+ + ）+ （1﹣m）﹣ 1

=﹣ （m+3）2+ ，

∵﹣ ＜0，

∴m=﹣3时，△PBD的面积最大，此时P（﹣3， ），Q（﹣3，0）．

如图2中，作Q关于y轴的对称点Q′，将Q′向左平移 个单位得到Q″，连接PQ″交抛物线对称轴于M，此时PM+MN+NQ最短．

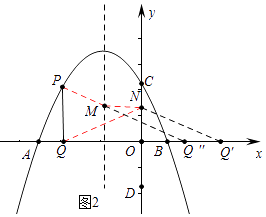
易证四边形MNQ′Q″是平行四边形，

∴NQ=NQ′=Q″M，

∴PM+MN+NQ=PM+MQ″+MN=PQ″+MN，

∵Q″（ ，0），

∴PQ″= = ，

∴PM+MN+NQ的最小值为 +

（3）解：如图3中，

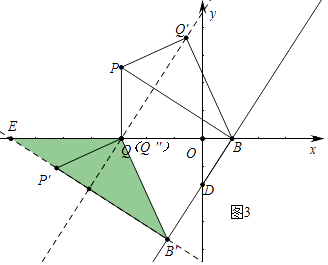
由（2）可知直线PB的解析式为y=﹣ x+ ，直线BD的解析式为y= x﹣ ，

易证∠PBQ=30°，∠DBO=60°，PB⊥BD．

①当点Q″与Q重合时，∵∠B′EQ=∠QB′E=30°，

∴EQ=B′Q″=4，

∴OE=QE+OQ=7．

②如图4中，当B′E=B′Q″时作B′N⊥x轴于N．

∵B′E=B′Q″=4，∠B′EN=30°，

∴B′N= B′E=2，EN=2 ，

∴B′（ ，﹣2），

∴OE=2 + = ﹣1．

③如图5中，当EQ″=EB′时，作B′N⊥x轴于N．

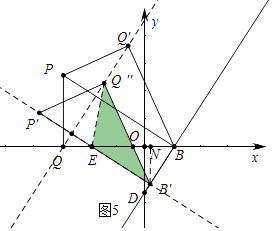
易知EP′=EQ″=EB′= ，B′N= ，EN=2，

∴B′（ ，﹣ ），

∴EO= ．

④如图6中，当B′E=B′Q″时，

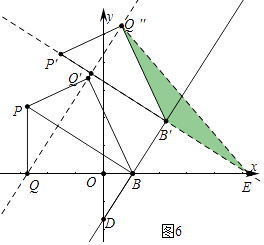
易知B′E=B′Q″=4，

在Rt△BEB′中，BE=EB′÷cos30°= ，

∴OE=OB+BE= +1，

综上所述，满足条件的OE的值为7或 ﹣1或 或 +1．

【解析】（2）利用函数思想解决最值问题，设出未知数，把△PDB分割成S△PDB=S△PDK+S△PBK﹣S△DKB，用m的代数式分别表示出三个三角形的面积，构建出函数，配成顶点时，求出最值；几条线段的和PM+MN+NQ最小值问题可利用对称法，把线段和转化为一条直线上的线段即可；（3）等腰三角形的分类，可就哪两条边是腰分类：B′E=B′Q；或点Q″与Q重合；或B′E=B′Q″或EQ″=EB′或B′E=B′Q″即可求出OE的长.