题目内容
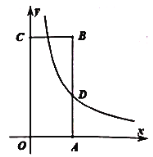
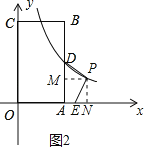
【题目】如图,矩形![]() 放置在平面直角坐标系上,点
放置在平面直角坐标系上,点![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的坐标是
的坐标是![]() ,其中
,其中![]() ,反比例函数y=
,反比例函数y=![]()
![]() 的图象交
的图象交![]() 交于点
交于点![]() .
.
(1)![]() _____(用
_____(用![]() 的代数式表示)
的代数式表示)
(2)设点![]() 为该反比例函数图象上的动点,且它的横坐标恰好等于
为该反比例函数图象上的动点,且它的横坐标恰好等于![]() ,连结
,连结![]() .
.
①若![]() 的面积比矩形
的面积比矩形![]() 面积多8,求
面积多8,求![]() 的值。
的值。
②现将点![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到点
得到点![]() ,若点
,若点![]() 恰好落在
恰好落在![]() 轴上,直接写出
轴上,直接写出![]() 的值.
的值.
【答案】(1)m﹣4;(2)①m2=16;②m=2+2![]() .
.
【解析】
(1)利用反比例函数图象上点的坐标特征可求出点D的坐标,结合点B的坐标可得出BD的长;
(2)①过点P作PF⊥AB于点E,则PF=m﹣4,由△PBD的面积比矩形OABC面积多8,可得出关于m的一元二次方程,解之取其正值即可得出结论;
②过点P作PM⊥AB于点M,作PN⊥x轴于点N,易证△DPM≌△EPN,利用全等三角形的性质及反比例函数图象上点的坐标特征,可得出关于m的方程,解之取其正值即可得出结论.
解:(1)当x=4时,y=![]() =4,
=4,
∴点D的坐标为(4,4),
∴BD=AB﹣AD=m﹣4.
故答案为:m﹣4.
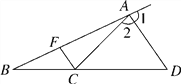
(2)①过点P作PF⊥AB于点E,则PF=m﹣4,如图1所示.
∵△PBD的面积比矩形OABC面积多8,
∴![]() BDPF﹣OAOC=8,即
BDPF﹣OAOC=8,即![]() (m﹣4)2﹣4m=8,
(m﹣4)2﹣4m=8,
整理,得:m2﹣16m=0,
解得:m1=0(舍去),m2=16.
②过点P作PM⊥AB于点M,作PN⊥x轴于点N,如图2所示.
∵∠DOM+∠MPE=90°,∠MPE+∠EPN=90°,
∴∠DPM=∠EPN.
在△DPM和△EPN中,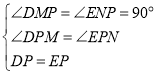 ,
,
∴△DPM≌△EPN(AAS),
∴PM=PN.
∵点P在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴点P的坐标为(m,![]() ),
),
∴PM=m﹣4,PN=![]() ,
,
∴m﹣4=![]() ,
,
解得:m1=2+2![]() ,m2=2﹣2
,m2=2﹣2![]() (舍去).
(舍去).
∴若点E恰好落在x轴上时,m的值为2+2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】学校组织八年级350名学生参加“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
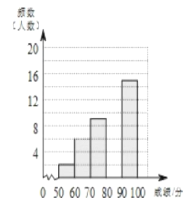
请根据所给信息,解答下列问题:
(1)求a和b的值;
(2)请补全频数分布直方图。