Question

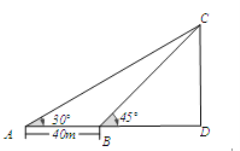
【题目】如图，小明在A处利用测角仪观测气球C的仰角为30°，然后他沿正对气球方向前进了40m到达B处，此时观测气球的仰角为45°．如果测角仪高度为1m，那么气球的高度是多少？（精确到0.1m）（备注：≈1.414，≈1.732）

Answer 1

【答案】气球的高度约为55.6m

【解析】设CD=xm.由锐角三角函数将AD、BD用含x的式子表示出来，再利用AD-BD=40列出方程，解之即可得出答案.

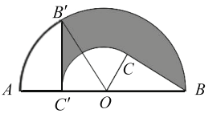
如图，点A、B、C分别表示观测点及气球的位置。

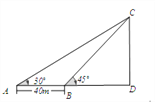
由题意知，∠CAD=30°，∠CBD=45°，CD⊥AD,AB=40m,设CD=xm.

在Rt△BDC中，由tan45°=,得BD= = x

在Rt△ADC中，由tan30°=,得AD== x.

∵AD-BD=40， ∴x- x=40.

∴x=20+20≈54.6.

由于测角仪的高度为1m，因此气球的高度约为55.6m.

答：气球的高度约为55.6m